图论–潘登同学的图论笔记(Python)

目录

• 1.图的数据结构
• 2.图的分类
  • 无向图
  • 有向图
  • 道路、回路与连通性
  • 欧拉图
  • 哈密顿图
  • 平面图
• 3.匹配
  • 独立数和支配数的关系
  • 匹配
  • 构成最大匹配的充要条件
  • 拉丁方
  • 边覆盖
  • 二部图的匹配
• 4.图的着色
• 5.网络与流
• 6.加餐部分
• 7.写在最后

图的数据结构

在数据结构中我们可以知道，图由节点和边构成，那么想实现图的数据结构就必然离不开节点Node，为了避免混淆，我的节点同一命名为Vertex；

那么实现Vertex需要一些什么属性和方法呢?

• 节点的名称
• 节点的与什么节点连接以及连接的权值
• 增加相邻节点(或者叫修改相邻节点的边权值)
• 获得相邻节点(就是通过这个节点知道他的相邻节点是什么)
• 获得节点名称(由Vertex对象获得自己的名称)
• 获得相邻边数据(通过相邻的节点的名称知道他们之间的权值)
• 显示设置(如果在命令行把Vertex输入, 显示的东西, 如果不写的话, 就会显示对象地址)

话不多说 上代码！

class Vertex:
    def __init__(self, key):
        self.id = key
        self.connectedTo = {}     # connectedTo用于储存相邻节点 key是相邻节点(对象而不是名称) value是连接权值

    def addNeighbor(self, nbr, weight=0):   # 增加相邻边，默认weight为0
        '''
        input:
            nbr: Vertex object
            weight: int
        return:
            None
        '''
        self.connectedTo[nbr] = weight

    def getConnections(self):   # 获得相邻节点
        '''
        input: None
        return: Vertex object
        '''
        return self.connectedTo.keys()

    def getId(self):   # 获得节点名称
        '''
        input: None
        return: key(str)
        '''
        return self.id
    
    def getWeight(self, nbr):   # 获得相邻边数据
        '''
        input: Vertex object
        return: weight(int)
        '''
        return self.connectedTo[nbr]
    
    def __str__(self):   # 显示设置(__str__是内置方法，也就是不需要显示的使用这个方法就可以用这个函数)
        return str(self.id) + 'connectTo:' + \
               str([x.id for x in self.connectedTo])


if __name__ == '__main__':
    # 与节点相关的数据, 链接表
    a_info = {'x1':['y3', 'y5']}
    # 新建节点
    x1 = Vertex('x1')
    y3 = Vertex('y3')
    y5 = Vertex('y5')
    # 根据邻接表添加相邻节点
    x1.addNeighbor(y3, 1)
    x1.addNeighbor(y5, 5)
    # 测试定义的函数功能
    # 获取节点id
    print(x1.getId())
    print(y5.getId())
    # 获取节点的相邻节点
    print(x1.getConnections())
    print(x1)
    # 由相邻节点获得与相邻节点的权值
    print(x1.getWeight(y5))

实现完节点了,接下来就是实现图了;

那么图的数据结构都包括什么呢?

• 图的一种储存数据的方式就是邻接表，采取邻接表来储存节点
• 图的节点个数
• 在图中增加节点
• 通过节点的key获得节点对象
• 判断节点在不在图中(in 内置函数)
• 新增两节点的边
• 获取所有节点的名称
• 迭代器的实现(通过for 循环把vertex对象取出)

话不多说 上代码！

import Vertex  # 导入上面写的代码
class Graph:
    def __init__(self):
        self.vertList = {}  # 这个虽然叫list但是实质上是字典
        self.numVertices = 0  # 记录节点个数

    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

	def getVertex(self, key):   # 通过key获取节点信息
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        if key in self.vertList:
            return self.vertList[key]
        else:
            return None

	def __contains__(self, n):  # 判断节点在不在图中
		'''
        input: Vertex key (str)
        return: bool
        '''
        return n in self.vertList

	def addEdge(self, from_key, to_key, cost=1):    # 新增边
		'''
        input:
            from_key: vertex key (str)
            to_key: vertex key (str)
            cost: int
        return:
            None
        '''
        if from_key not in self.vertList:      # 不再图中的顶点先添加
            self.addVertex(from_key)
        if to_key not in self.vertList:
            self.addVertex(to_key)
        # 调用起始顶点的方法添加邻边
        self.vertList[from_key].addNeighbor(self.vertList[to_key], cost)

	def getVertices(self):   # 获取所有顶点的名称
        return self.vertList.keys()

	def __iter__(self):  # 迭代取出
        return iter(self.vertList.values())  # 采用iter直接转成可迭代对象

	def __len__(self):  # 查看节点个数
        return self.numVertices

if __name__ == '__main__':
    # 邻接表
    g_dict ={'1':[['2', 10], ['3', 10]],
             '2':[['3', 2], ['4', 4], ['5', 8]],
             '3':[['5', 9]],
             '4':[['6', 10]],
             '5':[['4', 6], ['6', 10]]}
    # 创建graph对象
    g = Graph()
    # 在Graph中vertList的数据结构其实就是上面这个
    # 遍历g_dict
    for from_key in g_dict:
                for to_key in g_dict[from_key]:
                    g.addEdge(from_key, to_key[0], [0, to_key[1]])
    # 测试通过节点名称获取节点
    print(g.getVertex('3'))
    # 获得所有节点的名称
    print(g.getVertices())
    # 查看节点个数
    print(len(g))
    # 判断节点在不在图中
    print('7' in g, '3' in g)

OK!!, 现在我们已经成功实现了图的数据结构, 有了数据结构我们就可以用图的特性搞点事情了！！！

细心的同学已经注意到了, 上面刚刚出现了邻接表这个词语, 当然总是跟他相提并论的还有邻接矩阵,我们先把这两个概念说清楚；

图的邻接表

图的邻接表存储法。邻接表既适用于存储无向图，也适用于存储有向图；

在具体讲解邻接表存储图的实现方法之前，先普及一个”邻接点”的概念。在图中，如果两个点相互连通，即通过其中一个顶点，可直接找到另一个顶点，则称它们互为邻接点；

邻接指的是图中顶点之间有边或者弧的存在;

例如，存储图 1a) 所示的有向图，其对应的邻接表如图 1b) 所示：

拿顶点 V1 来说，与其相关的邻接点分别为 V2 和 V3，因此存储 V1 的链表中存储的是 V2 和 V3 在数组中的位置下标 1 和 2;

` 简化起见 `

我喜欢把邻接表定义为一个字典， 字典的keys储存出发点， values是一个长度为 2 的list, list的第一个元素表示到达点， 第二个元素表示weight

• 具体代码就是这样

  # 邻接表
  g_dict ={'1':[['2', 10], ['3', 10]],
     '2':[['3', 2], ['4', 4], ['5', 8]],
     '3':[['5', 9]],
     '4':[['6', 10]],
     '5':[['4', 6], ['6', 10]]}
  

  ‘1’:[[‘2’, 10], [‘3’, 10]] 就表示顶点’1’出发到达顶点’2’的权值是10， 到达顶点’3’的权值是10;

图的邻接矩阵

图的邻接矩阵大家都很熟悉, 就是用一个矩阵来表示点与点之间的关系, 沿用上面邻接表的例子;

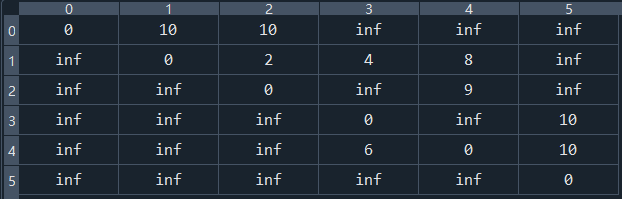
• 具体长这样

  import numpy as np
  np.array([[0, 10, 10, np.inf, np.inf, np.inf],
          [np.inf, 0, 2, 4, 8, np.inf],
          [np.inf, np.inf, 0, np.inf, 9, np.inf],
          [np.inf, np.inf, np.inf, 0, np.inf, 10],
          [np.inf, np.inf, np.inf, 6, 0, 10],
          [np.inf, np.inf, np.inf, np.inf, np.inf, 0]])
  

好了！我们已经介绍完图的数据结构了, 那现在我们开始系统的学习图论吧！！

图的分类

无向图(我们着重讨论简单图)

图的数学语言

根据前面数据结构的引入, 我们可以清楚的知道:图的由顶点, 边组成；

• 贯彻集合论的思想, 将点写成一个点集V, 边写成一个边集E;

  V = {v1,v2,v3,…,vn}

  E = {e1,e2,e3,…,em}

• 还有他们的对应关系呢！ 定义一个由E→V^2的映射r；

  r(e) = {u,v} ⊆ V

所以我们以后就用G = (V,E,r)来描述无向图了

` 接下来是用来描述图的术语 `

• 邻接

  假设G = (V,E,r)为无向图, 若G的两条边e1和e2都与同一个顶点相关联, 则称e1和e2是邻接的

• 自环,重边

  假设G = (V,E,r)为无向图,如果存在e,有r(e)={u,v}且u=v, 那么称e为一个自环

  假设G = (V,E,r)为无向图,若G中关联同一对顶点的边多于一条,则称这些边为重边

• degree(度)

  假设G = (V,E,r)为无向图,v∈V, 顶点v的度数dgree ged(v) 是G中与v关联的边的数目(说白了就是有多少个顶点跟v相连)

• 孤立顶点, 悬挂点,奇度点,偶度点

  假设G = (V,E,r)为无向图,G中度数为零的顶点称为孤立零点,

  图中度数为1的顶点成为悬挂点,与悬挂点相关联的边称为悬挂边,

  图中度数为k的点成为k度点,度数为奇数的为奇数点,度数为偶数的称为偶数点

简单图:不存在自环和重边的无向图

• 图的基本定理/握手定理
  • 假设G = (V,E,r)为无向图,则有∑deg(v) = 2|E|; 即所有顶点的度数是边的两倍

    这个的定理是显然的，因为一条边能连接两个顶点

  • 推论: 在任何无向图中,奇数度的点必为偶数个

    这个也很好证明，因为总的度数是偶数, 那想所有顶点的度数之和为偶数, 偶数个奇数度的顶点之和才能是偶数

• 例子: 问题如下: 假设有9个工厂, 求证:
  • (1)在他们之间不可能每个工厂都只与其他3个工厂有业务联系
  • (2)在他们之间不可能只有4个工厂与偶数个工厂有业务联系

    证明留给读者喔！

在简单图范畴下的其他有特点的图

• 零图,离散图

  G中全是孤立顶点, 也称0-正则图

• 正则图

  所有顶点度数都相同的图, 若所有顶点度数均为k, 则称k-正则图

• 完全图

  任意两个顶点都有边, 也称n-正则图

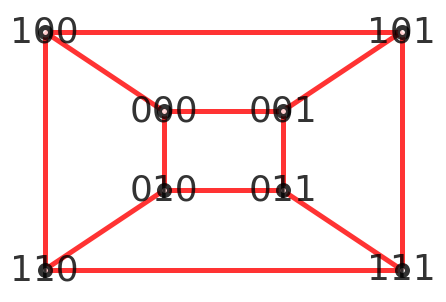
• n-立方体图

  其实长的就跟立方体一样,但由于图是平面的,下面给出严谨的数学定义 如果图的顶点集v由集合{0,1}上的所有长为n的二进制串组成,两个顶点的相邻当且仅当他们的标号序列仅在一位数字上不同 如图绘制了多个立方体图

• 大家也可以尝试自己构建(推荐一个构建网络的小工具networkx,但是networkx不是本文的主要工具,故不详细讲解,感兴趣的朋友们自己了解哦)
• 贴上代码

import networkx as nx
import matplotlib.pyplot as plt


G = nx.Graph()
points = {'100':['101', '110', '000'],
		  '110':['111', '100', '010'],
		  '000':['001', '010', '100'],
		  '001':['101', '011', '000'],
		  '011':['001', '111', '010'],
		  '101':['111', '100', '001'],
		  '111':['110', '101', '011'],
		  '010':['110', '011', '000']}
for i in points:
	for j in points[i]:
		G.add_edge(i, j)
 # 设置节点的位置
left = ['100', '110']
middle_left = ['000', '010']
middle_right = ['001', '011']
right = ['101', '111']

options = {
		"font_size": 36,
		"node_size": 100,
		"node_color": "white",
		"edgecolors": "black",
		"edge_color": 'red',
		"linewidths": 5,
		"width": 5,
		'alpha':0.8,
		'with_labels':True
	}
pos1 = {n: (0, 5-3*i) for i, n in enumerate(left)}
pos1.update({n: (1, 4-i) for i, n in enumerate(middle_left)})
pos1.update({n: (2, 4-i) for i, n in enumerate(middle_right)})
pos1.update({n: (3, 5-3*i) for i, n in enumerate(right)})
plt.clf()
nx.draw(G, pos1, **options)

• 一个3-立方体图如下:

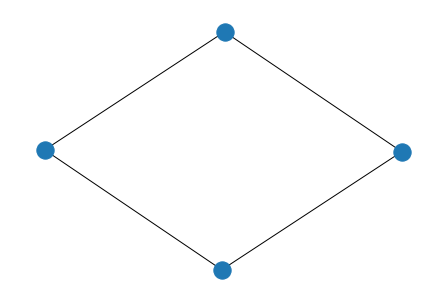
• 圈图

  假设V = {1,2,…,n} (n>2) E = {(u,v)| 1 ≤ u, v ≤ n, u-v ≡ 1(mods n)} 则称简单图为轮图

• 一个圈图如下：

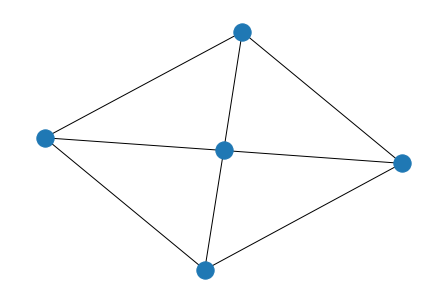
• 轮图

  假设V = {0,1,2,…,n} (n>2), E = {(u,v)| 1 1 ≤ u, v ≤ n, u-v ≡ 1(mods n) 或者 u=0, v>0} 则称简单图为轮图, 其实就是在圈图的基础上增加了一个顶点去连接所有点

• 一个轮图如下:

• 二部图(很经典)

  若简单图G = (V,E,r)的顶点V存在一个划分{V1, V2}使得G中任意一条边的两端分别属于V1和V2,则称G是二部图

  如果V1中每个顶点都与V2中每个顶点相邻, 则成为完全二部图

• 一个二部图如下:
• 一个完全二部图如下:

有向图

就是上面的无向图的边有了方向即边e = {u, v} 是一个有序对

• degree(度)

  上面已经介绍过度了, 但在有向图中我们要把他细分一下 deg(v) = deg(v)(-) + deg(v)(+)

  出度 : 以v为起始点的有向边的数目, 记为deg(v)(+)

  入度: 以v为终点的有向边的数目, 记为deg(v)(-)

• 定理

  对任意有向图G=(V,E,r), 有∑deg(v)(+) = ∑deg(v)(+) =

  E

• 赋权图

  假设G=(V,E,r)为图, W是E到R的一个函数,则称G为赋权图,对于e∈E,w(e)称作边e的权重或者简称权

  其实就是之前实现图的数据结构中的cost

图的同构与子图

• 同构

  设G1 = (V1,E1,r1)和G2 = (V2,E2,r2)是两个无向图

  如果存在V1到v2的双射f和E1到E2的双射g, 满足对任意的e∈E1,若r1(e)={u,v},则r2(g(e))= {f(u), f(v)} ,则称G1和G2是同构的,并记为G1≌G2

• 一对全等图的图像如下:

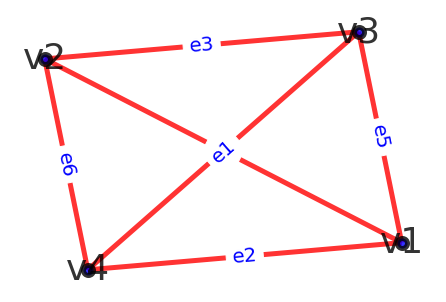
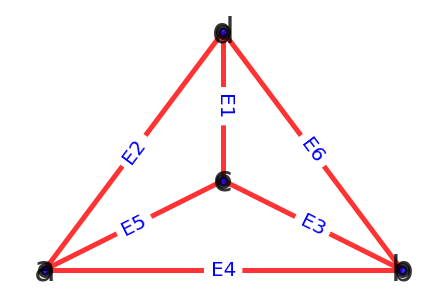
  点集之间的双射函数f(v1) = a, f(v2) = b, f(v3) = c, f(v4) = d,

  边集之间的双射函数f(ei) = Ei, i = 1,2,…,6

• 补图

  假设G=(V,E)是一个n阶简单图 令E’ = {(u,v)|u,v∈V, u ≠ v, {u,v}∉E} 则称(V, E’)为G的补图, 记作 G’ = (V,E’)

  若G与G’同构, 则称G为自补图

• 子图

  设G1 = (V1,E1,r1)和G2 = (V2,E2,r2)是两个图; 若满足V2 ⊆ V1, E1 ⊆ E2, 及r2 = r1|E2, 即对于∀e∈E2 有r2(e) = r1(e) ,则称G2是G1的子图

  • 当V1=V2时,称G2时G1的支撑子图(因为当把顶点看成构成这个图的支点,当支点与原本图都一样的时候就可以把他称为支撑子图)

  • 当E1 ⊆ E2 或 V2 ⊆ V1 时, 称G2是G1的真子图

  • 当V2 = V1 且 E2 = E1或E2 = ∅ 时, 称G2是G1的真子图

• 导出子图

  设G2 = (V2,E2,r2)是G1 = (V1,E1,r1)的子图,若E2={e

  r1(e)={u,v}⊆V2}(即E2包含了图G中V2的所有边)

构造子图的几种方法

• 在原图中删掉点和与他关联的边,(得到的图也叫删点子图)
• 在原图中删掉边(得到的是删边子图)

道路、回路与连通性

• 道路

  有向图G=(V,E,r)中一条道路Π 是指一个点-边序列V0,e1,v1,…,ek,vk,满足对于所有i=1,2,…,k r(ei) = (vi-1,vi) 称Π是从v0到vu的道路

• 回路

  如果上面的道路中v1 = vk, 就是回路

• 简单道路/简单回路

  如果道路/回路中各边互异,则称Π是简单道路/简单回路

  如果道路/回路中,除v0,vk外,每个顶点出现一次, 则称Π是初级道路/初级回路(也称圈)

• 定理

  假设简单图G中每个顶点的度数都大于1,则G中存在回路

证明: 假设Π:v0, v1, … ,vk-1,vk是图G中最长的一条初级道路,显然v0和vk都不会与不在道路Π上的任何顶点相邻,否则就会有一条更长的道路;

但是,deg(v0)>1,因此必定存在Π上的顶点vi与v0相邻,于是产生了回路

• 可达

  u,v是G中两个顶点,如果u=v或G中存在u到v的道路,则称u到v是可达的

• 连通图

  假设G是无向图,如果图中任意两相异点之间都存在道路,则称G是连通的或者连通图

• 连通分支(重要)

  假设无向图G=(V,E)的顶点集V在可达关系下的等价类为{v1, v2, …, vk},则G关于vi的导出子图称作G的一个连通分支(其中i=1,2,…,k)

  如果形象理解连通分支呢？ 我举一个通俗一点的例子好了

  就拿国家与国家之间的关系来理解好了, 一个国家可能有很大的疆域也可能只有很小的疆域; 但是在与其他的国家进行外交的时候,无论这个国家再小,都是以一个独立的身份与别国外交; 而无论某个国家的某个地区的实力再强大,也不能独立的与别国外交(即一个国家只会一个身份去与别国外交);

  而连通分支就是来描述这样一种情况, 在一个网络中, 有很多的顶点, 但是很多顶点都有共性(比如他们500年前是一家), 那么就可以把他们看成一个顶点,这样就方便分析了

  而这个共性具体来说就是; 互相可达(就是这一堆的任何顶点都可以达到另一个顶点(也要在网络内))

后面还会讲到怎么求解连通分支的kosaraju算法

• 一个包含三个连通分支的图如下:

• 割边(桥)

  假设G=(V,E,r)是连通图, 若e∈E,且G-e(从G中去掉边e)不连通,则称e是图G中的一条割边或桥

  如上图的7→9就是桥, 因为去掉之后图就不连通了

• 定理

  连通图中的边e是桥, 当且仅当e不属于图中任意的一条回路;(因为回路一定是有来又回,如果桥在回路里面,那把他去掉图仍然是连通的)

• 有向图的连通

  假设G是有向图,如果忽略图中边的方向后得到的无向图是连通的,则称G为连通的;否则就是不连通的

• 强连通, 单向连通

  有向连通图G, 对于图中任意两个顶点u和v,u到v 和 v到u都是可达的,则称G为强连通的; 如果图中任意两个顶点u和v, u到v 和 v到u至少之一是可达的,则称G为单向连通的

• 有向无环图(DAG)

  有向图G,如果图中不存在有向回路,则称G为有向无环图

欧拉图

• 欧拉图

其实欧拉图的来源是那个柯尼斯堡七桥问题,这不是本文重点,感兴趣的同学自行百度喔

通过图G中每条边一次且仅一次的道路称作该图的一条欧拉道路;(相当于一笔画)

通过图G中每条边一次且仅一次的回路称作该图的一条欧拉回路;(相当于头尾相连的一笔画)

存在欧拉回路的图称作欧拉图

• 一些例子如下:

• 欧拉图的充要条件

  无向图G是欧拉图当且仅当G是连通的而且所有顶点都是偶数度

证明: (必要性)假设G是欧拉图,即图中有欧拉回路,即对于任意一个顶点,有入必有出,因此每个顶点都是偶数度;

(充分性)设G的顶点是偶数度, 采用构造法证明欧拉回路的存在性:

从任意点v0出发,构造一条简单回路C, 因为各顶点的度数都是偶数, 因此一定能够回到v0, 构造简单回路;(!!!想清楚了再往下看!!!)

下一步,在上面构造的简单回路中挑一点再剩余的点和边中构造简单函数,重复该过程,直到不能再构造为止.

• 定理

  无向图G存在欧拉道路当且仅当G是连通的而且G中奇数度顶点不超过两个

证明: (必要性)G中一条欧拉道路L,在L中除起点和终点之外,其余每个顶点都与偶数条边(一条入,一条出)相关联. 因此, G中至多有两个奇数度的顶点

(充分性) ①若G中没有奇数度的顶点u,v,由上面定理,存在欧拉回路,显然是欧拉道路

②若G中有两个奇数度顶点u,v,那么连接uv,根据上面定理,可知存在一个欧拉回路C,从C中去掉边uv,得到顶点为u,v的一条欧拉道路(当我证到这的时候,应该有妙蛙妙蛙的声音)

(算法)构造欧拉回路 Fleury(G)

前提:得存在

输入: 至多有两个奇数度顶点的图G=(V,E,r)

输出:以序列的形式呈现欧拉回路/道路Π

算法流程:

① 选择图中一个奇数度的顶点v∈V,如果图中不存在奇数度顶点,则任取一个顶点v, 道路序列Π←v

② while |E| ≠ 0
    if 与v关联的边多余一条,则任取其中不是桥的一条边e:
    else 选择该边e:
        假设e的两个端点是v,u, Π←Π·e·u, v←u
        删除边e及孤立顶点(如果有)
③ 输出序列

• 定理

  假设连通图G中有k个度为奇数的顶点,则G的边集可以划分成 k/2 条简单道路,而不能分解为(k/2 - 1)或更少条道路

证明: (前半句) 由握手定理知k必为偶数.将这k个顶点两两配对,然后增添互不相邻的k/2条边,得到一个无奇数度顶点的连通图G’,

那么由前面的定理知,G’存在欧拉回路C,在C中删去增添的k/2条边, 便得到了k/2条简单道路;

(后半句) 假设图G的边集可以分为q条简单道路,则在图G中添加q条边可以得到欧拉图G’,因此图中所有顶点都是偶数度,而每添加一条边最多可以把两个奇数度顶点变为偶数度,即2q≥k

• 无向图的欧拉道路–推广–>有向图 定理

  有向图G中存在欧拉道路当且仅当G是连通的,而且G中每个顶点的入度都等于出度;

  有向图G中存在欧拉道路,但不存在欧拉回路当且仅当G是连通的;

  除两个顶点外,每个顶点的入度都等于出度,而且这两个顶点中一个顶点的入度比出度大1,另一个的入度比出度小1;

哈密顿图

• 哈密顿图

  图中含有哈密顿回路的图

• 哈密顿道路

  通过图G中每个顶点一次且仅一次的道路称作该图的一条哈密顿道路;

• 哈密顿回路

  通过图G中每个顶点一次且仅一次的回路称作该图的一条哈密顿回路;

• 注意

  1.图G中存在自环/重边不影响哈密顿回路/道路的存在性

  2.哈密顿图中一定不存在悬挂边

  3.存在哈密顿道路的图中不存在孤立顶点

• 例子: 科学家排座问题

  由七位科学家参加一个会议,已知A只会讲英语;B会讲英、汉;C会讲英、意、俄;D会日、汉;E会德、意;

  F会法、日、俄;G会讲德、法;安排他们坐在一个圆桌,使得相邻的科学家都可以使用相同的语言交流;

这就是一个很经典的哈密顿图的例子,转换一下,就是把他们之间的关系用图来表示,再在图中找一条哈密顿回路;

将讲相同语言的科学家之间连一条边,构造图,如下:

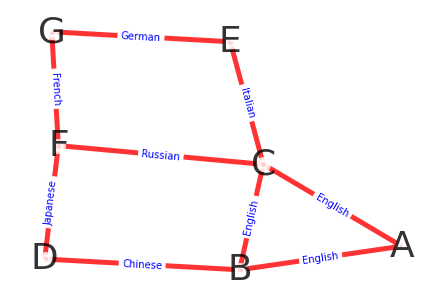
构图代码

# %%科学家排座问题
import networkx as nx
import matplotlib.pyplot as plt

G = nx.Graph()
a_dict = {'A':['English'],
          'B':['English', 'Chinese'],
          'C':['English', 'Italian', 'Russian'],
          'D':['Japanese', 'Chinese'],
          'E':['German', 'Italian'],
          'F':['French', 'Japanese', 'Russian'],
          'G':['German', 'French']}

# 用于储存相邻节点, key是语言， value是people_name
neighbors_dict = {}
for people_name in a_dict:
    G.add_node(people_name)
    for language in a_dict[people_name]:
        # 如果这个语言在neighbors_dict, 那么就把会这门语言的其他人
        # 与这个人之间连接一条边， 否则就把这个人会的语言加到dict中
        if language in neighbors_dict:
            for people_name_exist in neighbors_dict[language]:
                G.add_edge(people_name_exist, people_name, language=language)
            neighbors_dict[language].append(people_name)
        else:
            neighbors_dict[language] = [people_name]

options = {
        "font_size": 36,
        "node_size": 100,
        "node_color": "white",
        "edgecolors": "white",
        "edge_color": 'red',
        "linewidths": 5,
        "width": 5,
        'alpha':0.8,
        'with_labels':True
    }
pos = nx.spring_layout(G)
plt.clf()
nx.draw(G, pos, **options)

# 显示edge的labels
edge_labels = nx.get_edge_attributes(G, 'language')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10, font_color='blue')

再寻找一条回路经过所有顶点,这里我们采用DFS(深度优先搜索)

DFS深度优先搜索

DFS的本质是暴力搜索算法,也称回溯算法,就是一种在找不到正确答案的时候回退一步,再继续向前的算法

算法的思想很简单,但是实际操作可能会有点不好理解;下面我们通过几个小案例来深入理解DFS算法

• 例子1：

  全排列问题： 给出一个数字n，要求给出1-n的全排列,输出结果为列表

如给定数字3, 那结果就是[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

上代码!!!

# 回溯算法
def template(n):  # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
    result = []  # 这个保存结果

    def trace(path, choices):  # 递归函数
        '''
        path: 用于储存目前排列
        choices: 用于储存所有可选择的数字(1-n)
        '''
        if len(path) == n:  # 当path的长度等于输入的n时，结束算法，把结果加入结果列表
            result.append(list(path))
            return

        for item in choices:
            if item in path:  # 减枝操作(如果path里面有item这个数)
                continue
            path.append(item)  # 如果没有就把他加到目前的path中
            trace(path, choices)  # 递归调用自身
            path.pop()  # 撤销最后一次的选择继续向前找答案

    trace([], range(1, n+1))  # 调用函数trace
    return result

if __name__ == '__main__': 
    print(template(3))

观察到输出结果与上面预期一致,(回溯算法是后面很多算法的基础)

• 例子2:

  给定一个55的矩阵,里面有零元素,要求在矩阵里面5个0,使得每一行每一列都有零

  [[7, 0, 2, 0, 2],[4, 3, 0, 0, 0],[0, 8, 3, 5, 3],[11, 8, 0, 0, 4],[0, 4, 1, 4, 0]]

上代码!!!

#%%矩阵找零
import copy
def template(matrix):  # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
    result = []  # 这个保存结果

    def trace(path, choices):  # 递归函数
        '''
        path: dict 用于储存找到的零 key表示row values表示column
        choices: 矩阵matrix
        '''
        if len(path) == len(matrix):  # 当path的长度等于输入的n时，结束算法，把结果加入结果列表
            if path not in result:
                result.append(copy.deepcopy(path))
            return

        for row, items in enumerate(choices):
            for column, j in enumerate(items):
                if j == 0:  # 当元素为零时
                    if row in path.keys():
                        continue
                    if column in path.values():  # 减枝操作(如果path里面有column,说名这一列已经有零了)
                        continue
                    path[row] = column  # 如果没有就把他加到目前的path中
                    trace(path, choices)  # 递归调用自身
                    path.popitem()  # 撤销最后一次的选择继续向前找答案

    trace({}, matrix)  # 调用函数trace
    return result
if __name__ == '__main__':
    matrix = [[7, 0, 2, 0, 2],
              [4, 3, 0, 0, 0],
              [0, 8, 3, 5, 3],
              [11, 8, 0, 0, 4],
              [0, 4, 1, 4, 0]]
    print(template(matrix))

可以看到最终返回了两个结果:

[{0: 1, 1: 2, 2: 0, 3: 3, 4: 4}, {0: 1, 1: 3, 2: 0, 3: 2, 4: 4}]

表示的就是第0行选择第1列,第1行选择第2列,第2行选择第0列,第3行选择第3列,第4行选择第4列;带回矩阵验证发现符合条件

其实可以把例子2中的问题转换一下,又变成一个排列问题,仍然采用相同的方法求解

• 例子2(变形):

  在[2,4],[3,4,5],[1],[4,5],[1,5]中找到1-5的一个排列（如2，3，1，4，5）

  把所有可能的结果输出成列表

上代码!!!

#%%将矩阵找零问题转化
import copy
def template(a):
    result = []

    def trace(path,choices):
        if len(path) == len(choices):
            if path not in result:
                result.append(copy.deepcopy(path))
            return

        for row, items in enumerate(choices):
            if len(path) != row:  # path的元素的index对应choice的第几行
                continue  # 要是没有这一个if判断,path中储存的元素会乱
            for j in items:
                if j in path:
                    continue
                path.append(j)
                trace(path,choices)
                path.pop()  #删掉最后一个元素
    trace([],a)
    return result

if __name__ == '__main__':
    a = [[2,4],[3,4,5],[1],[3,4],[1,5]]
    print(template(a))

可以看到结果是一致的

• 例子3:给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合

上代码!!!

#%%77. 组合
# 给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        result = []
        def trace(path, choices, k):
            if len(path) == k:
                path = sorted(path)
                if path not in result:
                    result.append(path)
                return
            for items in choices:
                if items in path:
                    continue
                path.append(items)
                trace(path,choices, k)
                path.pop()
        
        trace([], range(1, n+1), k)
        return result

if __name__ == '__main__':
    print(Solution().combine(4, 2))

可以看到结果符合题意

经过上面几个例子的引入,同学们对回溯算法应该比较了解了,现在我们来完成科学家的排座问题吧!

科学家排座问题

• 修改数据结构,因为在DFS中要从一个点出发,遍历所有节点,为避免重复,对节点的数据结构加上color这个属性,标识为white，
• 对应的新增方法来修改color,以及查看color, 当节点已经被走过来就把他标识为gray,就不会再去遍历他;

话不多说,上代码!!!

#%% 科学家排座问题
from Vertex import Vertex # 导入Vertex
from Graph import Graph  # 导入之前实现的Graph

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.color = 'white'  # 新增类属性(用于记录节点是否被走过)

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

    # 新增方法
    def addUndirectedEdge(self, key1, key2, cost=1):
        self.addEdge(key1, key2, cost)
        self.addEdge(key2, key1, cost=1)

class Solution():   # 解决具体问题的类对象
    # 对科学家们创建图,之前有过相关操作
    def createGraph(self, a_dict):
        '''
        input: a_dict type: dict, key: people_name, value: language
        return: graph
        '''
        # 创建图
        graph = New_Graph()
        # 用于储存相邻节点, key是语言， value是people_name
        neighbors_dict = {}
        for people_name in a_dict:
            graph.addVertex(people_name)
            for language in a_dict[people_name]:
                # 如果这个语言在neighbors_dict, 那么就把会这门语言的其他人
                # 与这个人之间连接一条边， 否则就把这个人会的语言加到dict中
                if language in neighbors_dict:
                    for people_name_exist in neighbors_dict[language]:
                        graph.addUndirectedEdge(people_name_exist, people_name)
                    neighbors_dict[language].append(people_name)
                else:
                    neighbors_dict[language] = [people_name]
        return graph

    # 关键函数DFS,有
    def DFS(self, g, start):
       result = []
       # 深度优先搜索
       def trace(path, g, start):   # path是探索的路径 g是图，start是起始的节点
           start.setColor('gray')  # 将正在探索的节点设置为灰色
           path.append(start)
           # path中包含了所有顶点，且最后一个顶点到初始顶点要有路径就是最终结果
           if len(path) == len(g):
               if path[-1] in path[0].getConnections():
                   result.append(list(path))
               return
           else:
               for i in list(start.getConnections()):
                   if i.getColor() == 'white':  # 如果与他相邻的顶点还是白色,就探索他
                       trace(path, g, i)
                       path.pop()
                       i.setColor('white')    # 将已经撤销的结果的节点设置回白色

       trace([], g, start)
       return result

if __name__ == '__main__':
    a_dict = {'A':['English'],
              'B':['English', 'Chinese'],
              'C':['English', 'Italian', 'Russian'],
              'D':['Japanese', 'Chinese'],
              'E':['German', 'Italian'],
              'F':['French', 'Japanese', 'Russian'],
              'G':['German', 'French']}
    s = Solution()
    graph = s.createGraph(a_dict)
    path = s.DFS(graph, graph.getVertex('A'))
    # 因为是无向图，如果存在一个回路那一定会有两条路径
    for n in range(len(path)):
        for i in path[n]:
            print(i.getId(), end='-')
        print('\t')

看到最后输出了两个结果,表示科学家两两的相邻关系,带回题目,发现OK!!!

平面图

• 平面图

  如果可以将无向图G画在平面上,使得除端点处外,各边彼此互不相交,则称G是具有平面性的图(简称平面图)

• 欧拉公式

  面f、边m、顶点数n,的关系

  设G是一个面数为f(n,m)-连通平面图,则有n-m+f = 2

当然啦,欧拉公式已经像呼吸一样被我们所接受了,所以我这里就不证这种(1+1=2)的证明了,放一个链接:

• 欧拉公式的证明(生成树,对偶图)

• 图论意义下的欧拉公式（数学归纳法)

• 推论

  设G是一个面数为f的(n,m)平面图,且有L个连通分支,则 n-m+f = L+1

证明: 假设这L个分支是G1,G2, … ,GL,并设Gi的顶点数、边数和面数分别为ni,mi和fi;

显然有∑ni = n和∑mi = m; 此外, 由于外部面是各个连通分支共用的,因此∑fi = f + L - 1

由于每个Gi都是连通图，因此由欧拉公式有 ni - mi + fi = 2

于是有 n - m + f = ∑ni + ∑mi + ∑fi + 1 - L = ∑(ni - mi + fi) + 1 - L = 2L + 1 - L = L + 1

• e的细分

  假设G=(V,E,r)是无向图, e∈E,顶点u与v是边e的两端,e的细分是指在G中增加一个顶点w,删去边e,新增以u和w为端点的边e1以及w和v为端点的边e2

  就相当于原本有俩城市直接相连,然后现在找一个中继点,把这俩城市通过这个中继点连接

• 库拉托夫斯基定理

  一个无向图是平面图当且仅当他不包含与k5 (5阶完全图) 或 k3,3（完全3，3二部图)的细分同构子图

• 例子:
  • 求证: 彼得森图不是平面图

    先介绍一下彼得森图,是一个由10个顶点和15条边构成的连通简单图，它一般画作五边形中包含有五角星的造型。

一个经典的彼得森图如下:

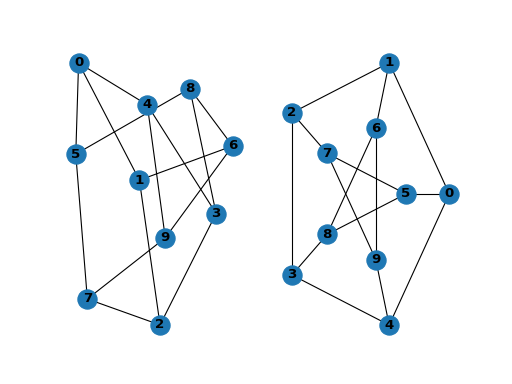
我们采用构图法证明:

左图是一个彼得森图,把中间的O点去掉,得到一个彼得森图的子图.

将这个子图看成一个K3,3的细分同构 (由K3,3构造中间的图的方式是: 去掉边BC,增加顶点A,去掉边DH、EI, 增加顶点F, G)

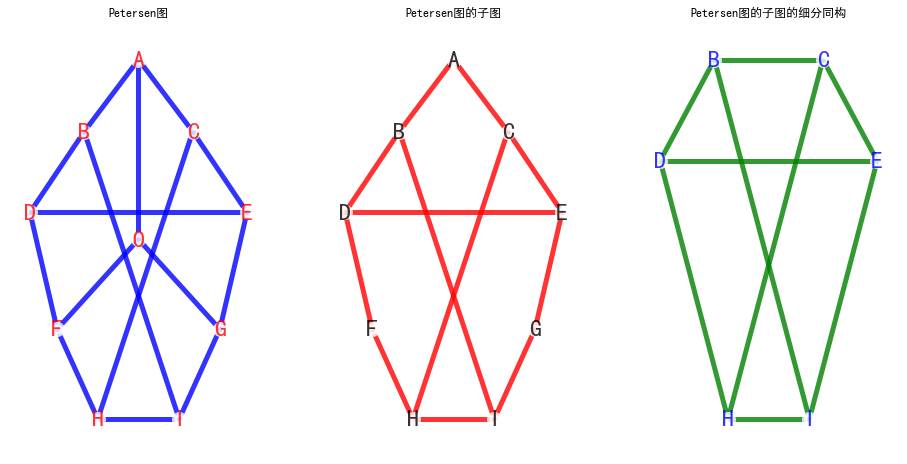
• 上图代码

#%%彼得森图不是平面图的证明
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
G = nx.Graph()
points = {'A':['B', 'C', 'O'],
          'B':['A', 'D', 'I'],
          'C':['A', 'E', 'H'],
          'D':['B', 'E', 'F'],
          'E':['C', 'D', 'G'],
          'F':['D', 'H', 'O'],
          'G':['E', 'I', 'O'],
          'H':['F', 'I', 'C'],
          'I':['G', 'H', 'B'],
          'O':['A', 'G', 'F']}

for i in points:
    for j in points[i]:
        G.add_edge(i, j)

points_1 = ['A']
points_2 = ['B', 'C']
points_3 = ['D', 'E']
points_4 = ['F', 'G']
points_5 = ['H', 'I']
points_6 = ['O']

options = {
        "font_size": 24,
        "node_size": 100,
        "node_color": "white",
        "edgecolors": "white",
        "edge_color": 'blue',
        "font_color": 'red',
        "linewidths": 5,
        "width": 5,
        'alpha':0.8,
        'with_labels':True
    }

pos = {n: (2, 5) for i, n in enumerate(points_1)}
pos.update({n: (1+2*i, 4.2) for i, n in enumerate(points_2)})
pos.update({n: (4*i, 3.3) for i, n in enumerate(points_3)})
pos.update({n: (0.5+3*i, 2) for i, n in enumerate(points_4)})
pos.update({n: (1.25+1.5*i, 1) for i, n in enumerate(points_5)})
pos.update({n: (2, 3) for i, n in enumerate(points_6)})



plt.figure(figsize=(16,8))
plt.subplot(131)
nx.draw(G, pos, **options)
G.remove_node('O')
plt.title('Petersen图')

plt.subplot(132)
pos.pop('O')
options['edge_color'] = 'red'
options['font_color'] = 'black'
nx.draw(G, pos, **options)
plt.title('Petersen图的子图')

plt.subplot(133)
G3_3 = G = nx.Graph()
points3_3 = {'B':['D', 'C', 'I'],
          'C':['B', 'E', 'H'],
          'D':['B', 'E', 'H'],
          'E':['C', 'D', 'I'],
          'H':['C', 'D', 'I'],
          'I':['E', 'H', 'B']}

for i in points3_3:
    for j in points3_3[i]:
        G3_3.add_edge(i, j)

pos1 = {n: (1+2*i, 4.2) for i, n in enumerate(points_2)}
pos1.update({n: (4*i, 3.3) for i, n in enumerate(points_3)})
pos1.update({n: (1.25+1.5*i, 1) for i, n in enumerate(points_5)})

options['edge_color'] = 'green'
options['font_color'] = 'blue'
nx.draw(G3_3, pos1, **options)
plt.title('Petersen图的子图的细分同构')

• 可平面图与哈密顿图存在联系

  如果简单图G既是哈密顿图又是平面图,那么在G画为平面图后,

  G的不在哈密顿回路C中的边落在两个集合之一: C的内部或C的外部

• (算法）哈密顿图的可平面性判断算法 QHPLanar(G)

输入: (n, m)-简单哈密顿图G

输出: True or False

① 将图G的哈密顿回路哈在平面形成一个环,使得C将平面划分为内部区域和外部区域

② 设G的不在C中的边e1,e2,…,e(m-n), 在新的图G’中构造顶点(顶点就是这个m-n个)

③ 若ei和ej在G的新画法中必须是交叉的,即他们二者无法同时画在C的内部或者外部,则在图G’的顶点ei和ej中连一条边

④ 若G’是二部图, 则输出T, 否则输出F

• 因为涉及到了两个边的画法问题,潘登同学暂时不能做算法实现0.0

• 算法例子: (判断G是否可平面)

左图是题目图G，判断是否可平面

中图是将图G画在平面上形成一个环, 右图是将e构造顶点形成新的图

发现新的图是一个二部图, 所以G可平面

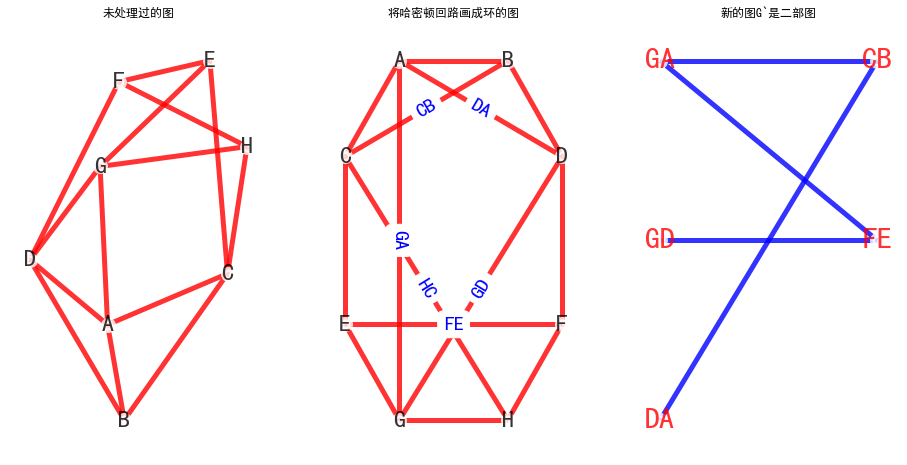
• 上图代码

#%%可平面性的判定例子
G = nx.Graph()
points_1 = {'A':['B', 'C', 'D', 'G'],
          'B':['A', 'D', 'C'],
          'C':['A', 'E', 'B'],
          'D':['B', 'A', 'F', 'G'],
          'E':['C', 'F', 'G'],
          'F':['D', 'E', 'H'],
          'G':['E', 'A', 'D', 'H'],
          'H':['G', 'F', 'C']}
# 用于显示边
G_edge = nx.Graph()
points_edge = {'A':['D', 'G'],
              'B':['C'],
              'C':['B'],
              'D':['A', 'G'],
              'E':['F',],
              'F':['E',],
              'G':['A', 'D',],
              'H':['C']}

G_bin = nx.Graph()
points_bin = {'GA': ['CB', 'FE'],
              'GD': ['FE'],
              'DA': ['CB']}

for i in points_1:
    for j in points_1[i]:
        G.add_edge(i, j)

for i in points_edge:
    for j in points_edge[i]:
        G_edge.add_edge(i, j, name=i + j)

for i in points_bin:
    for j in points_bin[i]:
        G_bin.add_edge(i, j)

points_1 = ['A', 'B']
points_2 = ['C', 'D']
points_3 = ['E', 'F']
points_4 = ['G', 'H']

pos = {n: (1+i, 5) for i, n in enumerate(points_1)}
pos.update({n: (0.5+2*i, 4.2) for i, n in enumerate(points_2)})
pos.update({n: (0.5+2*i, 2.8) for i, n in enumerate(points_3)})
pos.update({n: (1+i, 2) for i, n in enumerate(points_4)})

options = {
        "font_size": 24,
        "node_size": 100,
        "node_color": "white",
        "edgecolors": "white",
        "edge_color": 'red',
        "font_color": 'black',
        "linewidths": 5,
        "width": 5,
        'alpha':0.8,
        'with_labels':True
    }
plt.figure(figsize=(16, 8))
plt.subplot(131)
nx.draw(G, **options)

plt.title('未处理过的图')

plt.subplot(132)
nx.draw(G, pos, **options)
edge_labels = nx.get_edge_attributes(G_edge, 'name')
nx.draw_networkx_edge_labels(G_edge, pos, edge_labels=edge_labels, 
                             font_size=20, font_color='blue')
plt.title('将哈密顿回路画成环的图')

plt.subplot(133)
points_bin1 = ['GA', 'GD', 'DA']
points_bin2 = ['CB', 'FE']

pos_bin = {n: (1, 5-2*i) for i, n in enumerate(points_bin1)}
pos_bin.update({n: (3, 5-2*i) for i, n in enumerate(points_bin2)})

options_bin = {
        "font_size": 30,
        "node_size": 100,
        "node_color": "white",
        "edgecolors": "white",
        "edge_color": 'blue',
        "font_color": 'red',
        "linewidths": 5,
        "width": 5,
        'alpha':0.8,
        'with_labels':True
    }

nx.draw(G_bin, pos_bin, **options_bin)
plt.title('新的图G`是二部图')

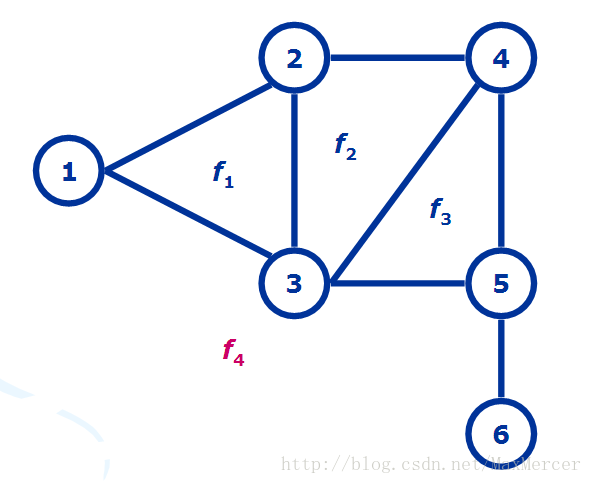
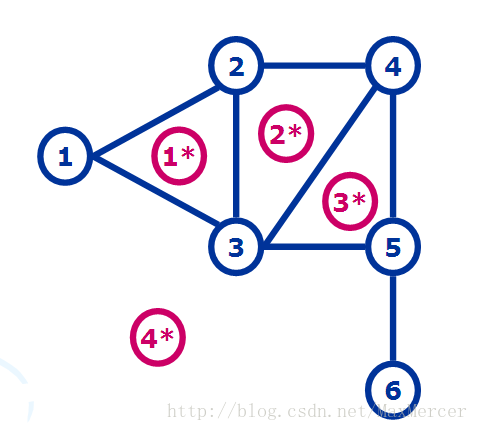
• 对偶图

  设G是一个平面图,满足下列条件的图G’称为G的对偶图

  • G的面f与G’的顶点V’ 一 一对应
  • 若G中的面fi和fj邻接于共同边界e,则在G’中有与e一 一对应的边e’,其以fi和fj所对应的点vi’和vj’为两个端点
  • 若割边e处于f内,则在G’中f所对应的点v有一个自环e’与e一 一对应

下面是几个对偶图的图：

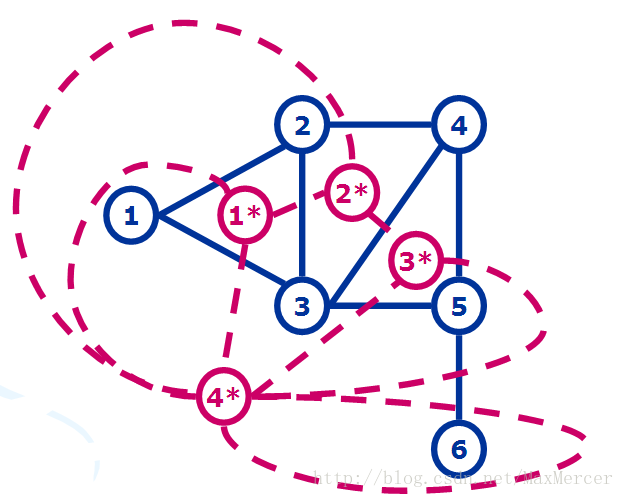
• 对偶图的画法

  ①在图G中每个面内画一个顶点

  ② 在这些新的顶点之间添加边,每条新的边恰好与G中一条边相交一次

下面是一个例子:

我们看到对偶图中出现了一个自环, 然后回去看原图的桥,发现就是那一个仅有的桥造成了这个自环

(注: G的桥与G’的自环, G的自环与G’的桥 存在对应关系)

• 图的平面性的应用:

  高速公路的设计 电路印刷板的设计中避免交叉

匹配

• 顶点支配,独立与覆盖 (前提假设,G是没有孤立顶点的简单图)

  设G = (V,E)是无向简单图, D⊆V, 若对于任意 v∈V-D，都存在u∈D，使得uv∈E,则称D为一个支配集

  若D是图G的支配集，且D的任何真子集都不再是支配集,则称D为一个极小支配集；

  若图G的支配集D满足对于G的任何支配集D’都有

  D

  ≤

  D’

  ,则称D为G的一个最小支配集(不唯一)

  最小支配集的元素个数称为图G的支配数

(注：极小支配集不一定是最小支配集，但是最小支配集一定是极小支配集)

• 例子1:

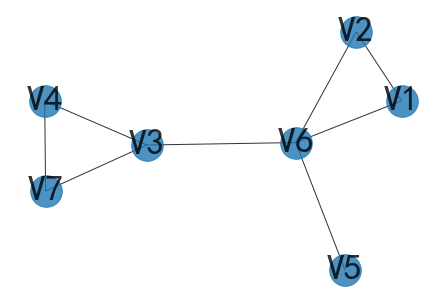
{v5,v6,v7}是支配集

{v6,v7}是极小支配集,也是最小支配集

{v3,v6}是极小支配集,也是最小支配集

• 例子2：

  (a)在任一简单图G(V,E)中,V是支配集

  (b)完全图Kn（n≥3）的支配数为1

  (c)完全二部图Km,n的支配数为min(m,n)

  (d)轮图Wn(n≥3)的支配数为1 （因为轮图中有一个点连接所有点)

• 独立集

  设G=(V,E,r)是一个无向图, S⊆V ,若对于任意的u,v∈S, 都有u与v不相邻, 则称S是G的一个点独立集或简称独立集(∅是任意图的独立集)

  若对G的任何独立集T，都有S⊄T,则称S是G的一个极大独立集；

  具有最大基数的独立集为最大独立集,其中点的个数称为G的独立数

注：(a) 极大点独立集不是任何其他点独立集的子集

(b)若点独立集S是G的一个极大独立集,则对于任意u∈V-S,都存在v∈S,使得u与v相邻

(c)最大独立集,极大独立集 都是不唯一的

(d)最大独立集是极大, 但极大不一定是最大

• 例子：

  (a) 完全图Kn(n≥3)的独立数为1

  (b) 完全二部图Km,n的支配数为max(m,n)

  (c) 圈图Cn(n≥3)的独立数为 floor(n/2)(向下取整) (隔一个取一个)

  (d) 轮图Wn(n≥3)的独立数为 floor(n/2)(向下取整) (隔一个取一个)

独立数和支配数的关系

• 定理

  一个独立集也是支配集当且仅当他是极大独立集

证明: (充分性)假设S是图的一个极大独立集,他不是支配集,则存在顶点v与S中所有顶点都不相邻,这与S作为独立集的’极大性’相矛盾;

(必要性)如果S是独立集也是支配集,但不是极大独立集,则有独立集S1,满足S⊆S1,考虑顶点u∈S1-S,则u与S中所有顶点都不相邻,这与S是支配集矛盾;

• 定理

  无向简单图的极大独立集也是极小支配集(反之不然)

证明: (若S是图的极大独立集, 显然是支配集)

下证: 其为极小支配集

(反证法) 若s不是极小支配集,则存在集合S1⊆S,S1也是支配集,考虑顶点u∈S1-S, 则u必与S1中的某顶点相邻,与S是独立集相矛盾；

(反之不然)可以看回上例子1 ， {v3,v6}是极小支配集但显然不是独立集

• 点覆盖 （用点去覆盖边）

  设G(V,E)是简单图, V’⊆V, 如果对于任意e∈E,都存在v∈V’,使得v是e的一个端点，则称V’是G的一个点覆盖集，简称点覆盖

  若V’是图G的点覆盖,且V’的任何真子集都不再是点覆盖,则称V’是一个极小点覆盖

  如果图G的点覆盖V’满足对于G的任何点覆盖V’‘都有

  V’

  ≤

  V’’

  ，则称V’是G的一个最小覆盖,其V’中元素个数称作覆盖数，记为β(G)

• 例子:

  (a)在任一简单图G(V,E)中,V是点覆盖

  (b)完全图Kn（n≥3）的覆盖数为1

  (c)完全二部图Km,n的覆盖数为min(m,n)

  (d)圈图Cn(n≥3)的覆盖数为 ceiling(n/2)(向上取整)

  (e)轮图Wn(n≥3)的覆盖数为 ceiling(n/2) + 1(向上取整)

• 定理

  在简单图G(V,E)中, V’⊆V是点覆盖集当且仅当V-V’是独立集

证明：（必要性）假设 V’⊆V是点覆盖集,若V-V’是不独立集,则存在顶点u,v∈V-V’，使得u，v相邻,而这与V’是点覆盖集产生矛盾（因为边uv没有被覆盖）

（充分性）如果V-V’是独立集, 但V’⊆V不是点覆盖集, 则存在边uv∈E, 使得u，v ∉ V’，于是u，v∈V-V’;而u，v相邻与V-V’是独立集相矛盾;

妙蛙妙蛙！！！！

前面的铺垫都差不多了,接下来进入正题了

匹配

设G=（V，E)是简单图, M⊆E， 如果M中任何两条边都不邻接,则称M为G的一个匹配或边独立集

设顶点v∈V，若存在e∈M，使得v是e的一端点,则称v是M-饱和的，否则称v是M-非饱和的

• 最大匹配数

  若匹配M满足对任意e∈E-M，M∪{e，}(这个逗号是显示问题) 不再构成匹配,则称M是G的一个极大匹配(不唯一)

  如果图G的匹配M满足对于G的任何匹配M都有

  M

  ≥

  M’

  ，则称M是G的一个最大基数匹配或最大匹配 或 最大匹配，最大匹配的元素个数称为图G的匹配数（记为V（G））

• 完全匹配 （把所有顶点都用上）

  饱和图中每个顶点的匹配称作完全匹配或完全匹配

注：（a) 在完美匹配中，每个顶点都关联匹配中的一条边；

(b)如果图G存在完美匹配,则图G的匹配数为G的阶数的一半,此时的阶数为偶数(不一定所有图都有完美匹配)

(c)每个完美匹配都是最大匹配,但最大匹配不一定是完美匹配

• 例子：

  (a) 完全图Kn(n≥3)的匹配数为 floor（n/2）

  (b) 完全二部图Km,n的匹配数为min(m,n)

  (c) 圈图Cn(n≥3)的匹配数为 floor(n/2)(向下取整)

  (d) 轮图Wn(n≥3)的匹配数为 ceiling(n/2)(向上取整)

构成最大匹配的充要条件

• 交错道路

  设M是G中一个匹配, 若G中一条初级道路是由M中的边和E-M中的边交替出现组成的,则称其为交错道路

一条交错道路如下图,绿色的一个匹配，从B1一直到A5的一条红绿相间的道路就是交错道路

• 可增广道路

  若一条交错道路的始点和终点都是非饱和点,则称其为M-可增广道路 (注：可增广道路的长度是奇数)

• 伯奇引理

  匹配M为图G = （V，E）的最大匹配当且仅当G中不存在M-可增广道路

证明:(必要性)假设M是最大匹配,且存在一条M-可增广道路e1,e2,…,e2k+1，则e2,e4,…,e2k+1为属于M的边e1,e2,…,e2k+1为不属于M的边;

构造新集合M1 =（M-{e2,e4,….e2k})∪{e1,e2,…,e2k+1}； 易证M1也是G的一个匹配。但

M1

=

M

+ 1,与M为最大匹配相矛盾

(也可以之间看特殊情况：{e1, e3, …, e2k+1}构成的匹配数就是

M

+1)

(充分性)如果G中不存在M-可增广道路,而M不是最大匹配，则必有最大匹配M1;

令M2 = M1 ∪ M, 则（新构造）图（V，M2）中所有顶点度数不超过2, 因此图（V,M2)中每个连通分支要么是一个单独的回路（要么是一个单独的道路）而且道路是交错的

由于

M1

>

M

, 因此M2中原本属于M1的边多余原本属于M的边。所以一定存在一条交错道路以M1的边开始.以M1的边结束,于是它就是一条M-可增广道路;

• 邻接顶点集

  设W是图G的顶点集的一个子集,则Ng（w) = {v

  存在u∈w， 使得u与v相邻}称作W的邻接顶点集

• (算法)最大匹配算法 MaxMatch(G)

输出：二部图 G = （X,Y,E)

输出: G的一个最大匹配M

① 任选一个初始匹配,给饱和顶点标记为1，其余为0

② while X中存在0:
    2.1 选择一个0标记点x∈X, 令u←{x}, v←∅
    2.2 若Ng(u) = v, 则x无法作为一条增广道路的端点,给x标记为2, 转②
    2.3 否则，选择y∈Ng(u) - v
        2.31 若y的标记为1，则存在边yz∈M，令u←u∪{z}， v←v∪{y},转 2.2
        2.32 否则,存在一条x至y的可增广道路P,令M←M∪P,给x和y标记1, 转②

（注：算法中标记1表示已饱和的顶点， 0表示未处理的顶点)

在写算法之前当然还要处理一下数据结构,对Vertex节点对象新增labels属性,在增加修改labels的方法和获取labels的方法

再重写一个二部图的数据结构Bin_Graph，与Graph的主要区别就是把节点分别储存到两个字典中了,所以整个数据结构要重写,不过万变不离其宗

话不多说，上代码!!!

#%%最大匹配
from Vertex import Vertex  # 导入Vertex

class New_Vertex(Vertex):
    def __init__(self,key):
        super().__init__(key)
        self.labels = 0   # 新增类属性(节点标记)

    # 新增类方法 设置标记
    def setlabel(self, label):
        self.labels = label

    # 新增类方法 获得标记值
    def getlabel(self):
        return self.labels

class Bin_Graph():
    # 这里因为要划分X与Y的点集，所以重写一个图的数据解构,与原本的Graph区别也不太大
    def __init__(self):
        self.x_vertList = {}  # 储存x的顶点
        self.y_vertList = {}  # 储存y的顶点
        self.numVertices = 0

    def addVertex(self, key, label):   # 增加节点
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        if label == 'x':
            self.x_vertList[key] = newVertex
        elif label == 'y':
            self.y_vertList[key] = newVertex
        return newVertex

    def getVertex(self, key):   # 通过key获取节点信息
        if key in self.x_vertList:
            return self.x_vertList[key]
        elif key in self.y_vertList:
            return self.y_vertList[key]
        else:
            return None

    def __contains__(self, n):  # 判断节点在不在图中
        return n in self.x_vertList or n in self.y_vertList

    def addEdge(self, from_key, to_key, label, cost=1):    # 新增边
        if (from_key not in self.x_vertList) and (from_key not in self.y_vertList):
            return print('from_key不在图中！！')

        if (to_key not in self.x_vertList) and (to_key not in self.y_vertList):
            return print('to_key不在图中！！')
        # 调用起始顶点的方法添加邻边
        if label == 'x':
            self.x_vertList[from_key].addNeighbor(self.y_vertList[to_key], cost)
        elif label == 'y':
            self.y_vertList[from_key].addNeighbor(self.x_vertList[to_key], cost)

    def addUndirectedEdge(self, key1, key2, cost=1):
        self.addEdge(key1, key2, 'x', cost)
        self.addEdge(key2, key1, 'y', cost=1)

    def get_x_Vertices(self):   # 获取所有x顶点的名称
        return self.x_vertList.keys()

    def get_y_Vertices(self):   # 获取所有y顶点
        return self.y_vertList.keys()

    def __iter__(self):  # 迭代取出
        return iter(list(self.x_vertList.values()) + list(self.y_vertList.values()))

    def __len__(self):
        return self.numVertices


class Solution():   # 解决具体问题的类对象
    # 创建二部图
    def createBinpartiteGraph(self, a_dict):
        '''
        
        Parameters
        ----------
        a_dict : dict对象,keys用于存放X,Values用于存放Y

        Returns
        -------
        bin_Graph : Bin_Graph二部图对象

        '''
        bin_Graph = Bin_Graph()
        for i in a_dict:
            bin_Graph.addVertex(i, 'x')
            for j in a_dict[i]:
                # 如果y不在图中就先添加
                if j not in bin_Graph.get_y_Vertices():
                    bin_Graph.addVertex(j, 'y')
                bin_Graph.addUndirectedEdge(i, j)
        return bin_Graph

    # 求出邻接顶点集
    def Ng(self, w, g):
        '''
        w:图g的一个顶点集的子集, 其中元素表示的是节点的名称
        return: w的邻接顶点集, 其中的元素表示的是节点的名称
        '''
        neighbors = []
        for i in w:
            temp = list(g.getVertex(i).getConnections())
            neighbors += [i.getId() for i in temp]
        return neighbors

    # 算法实现(最大匹配)
    def MaxMatch(self, g):
        '''
        g: 二部图
        return: 最大匹配m 字典，keys表示y values表示x
        '''
        m = {}
        # 如果x的顶点里面有0标记的
        while (0 in [g.getVertex(i).getlabel() for i in g.get_x_Vertices()]):
            # 选择一个标记为0的x
            for x in g.get_x_Vertices():
                if g.getVertex(x).getlabel()  == 0:
                    # U中装的是节点的keys
                    U = [x]
                    V = []
                    neibor = self.Ng(U, g)
                    while True:  # 这里设置while循环因为下面要回来这里
                        turn130while = False
                        # 如果Ng(U, g)=V, 则x无法作为一条可增广道路的端点，将x标记为2
                        if neibor == V:
                            # 将x标记为2
                            g.getVertex(U[0]).setlabel(2)
                            # 退回到130行while
                            turn130while = True
                            break
                        else:
                            turn130while = False
                            # 选择y属于neibor - V
                            diff = [i for i in neibor if i not in V]
                            for y in diff:
                                if g.getVertex(y).getlabel() == 1:
                                    # 修改U，V
                                    if m[y] not in U:
                                        U.append(m[y])
                                    if y not in V:
                                        V.append(y)
                                    # 退回到138行while循环
                                    break
                                else:
                                    turn130while = True
                                    # 把x，y加到可增广道路
                                    m[y] = x
                                    # 修改x，y的标记
                                    g.getVertex(x).setlabel(1)
                                    g.getVertex(y).setlabel(1)
                                    # 退回到130while循环 需要两步
                                    break
                            if turn130while:
                                break
                    if turn130while:
                        break
        return m

if __name__ == '__main__':
    a_dict = {'x1':['y3', 'y5'],
                            'x2':['y1', 'y2', 'y3'],
                            'x3':['y4'],
                            'x4':['y4', 'y5'],
                            'x5':['y5']}
    s = Solution()
    g = s.createBinpartiteGraph(a_dict)
    print(s.MaxMatch(g))

结果输出了 {‘y3’: ‘x1’, ‘y1’: ‘x2’, ‘y4’: ‘x3’, ‘y5’: ‘x4’}，这就是一个最大匹配,在下图（就是本题的二部图)中找不到更大的匹配比找到的这个匹配多；

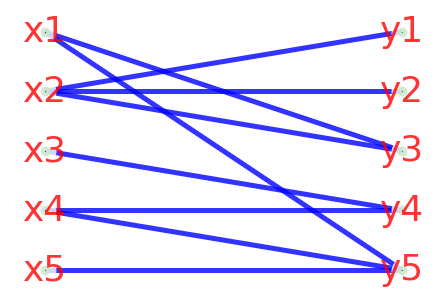
• 霍尔定理

  设G=(X,Y,E)为二部图,G中存在使X中每个顶点饱和的匹配M(即

  M

  =

  X

  ) 当且仅当对任何非空集合S⊆X,

  Ng(s)

  ≥

  S

  （该条件表示任意子集都有足够多的相邻顶点)

证明: (必要性)假定存在匹配M⊆E使得X中每个顶点饱和，则

Ng(S)

≥

N(X,Y,M)(S)

=

s

((X,Y,M)表示二部图G)

(充分性)假设M是一个最大匹配,且存在M-非饱和顶点x∈X；

① 如果x是孤立顶点，则

Ng({x})

= 0 < 1 =

{x}

, 与条件矛盾

② 否则,考虑所有从x开始的交错道路,记Y中所有x可以通过这些道路到达的顶点为集合T,记X中所有x可以通过这些道路到达的顶点为集合W， 由于所有从x开始的极长的（不能再延长）交错道路的终点都不能是Y中M-非饱和顶点(否则将产生M-可增广道路,与M是最大匹配矛盾)所以T中顶点都是M-饱和顶点。

记R为从x开始的所有交错道路的边形成的集合，则R∩M中的边构成了W-{x}和T中顶点一 一对应，

W-{x}

=

T

下证: Ng(W) = T

（反证法） 存在y∈Ng（W）-T，则 存在z∈W，使得zy∈E， 又因为W-{x}和T中元素都是M-饱和点或X本身，因此zy ∉ M

于是，要么x就是z；要么x可以通过某条交错道路到达z，再经过边zy可以到达y； 这都与y ∉ T矛盾；

最后，

w

=

W-{x}

+ 1 >

W-{x}

=

T

=

Ng(W)

与 条件（

Ng(s)

≥

S

）相矛盾 （证毕）

（虽然上面说了这么唬人的一大堆,但是这个定理想说明白的事情很简单,就是现在由一堆男的和一堆女的进行约会的匹配, 想要让男的都能有约会对象的充要条件就是男的认识足够多的女的,如:一个男的至少认识一个女的（或者更多））

• 推论

  设G = (X,Y,E)为二部图，若存在正整数K，使得对任意x∈X，由deg(x)≥k，对任意y∈Y， 由deg(x) ≤ k,则G中存在使X中每个饱和点的匹配.

证明: 假设非空集合S⊆X,则S中顶点关联的边至少K

S

条，而这些边都与Ng(S)中的顶点相关联,由于Y中顶点度数都不超过K，因此

Ng(S)

≥ K

S

/ K =

S

.所以存在使X中每个顶点饱和的匹配

• 推论

  对任意正整数k,k-正则二部图中必定存在使X中每个顶点饱和的匹配

直观例子(以2-正则二部图为例)

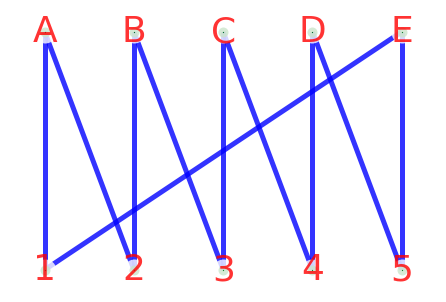
拉丁方

霍尔定理的应用

• 称每行每列都包含给定的n个符号恰一次的n阶方阵为拉丁方

• 例子：集合{1，2，3，4}的4阶拉丁方

L1 = [[1,2,3,4],[2,3,4,1],[3,4,1,2],[4,1,2,3]] L2 = [[1,2 3,4],[3,4,1,2],[4,3,2,1],[2,1,4,3]]

• (算法）构造拉丁方

  （书上讲得很繁琐)我设计一个算法就是先随机构建一个序列，然后后面的每一行都是把整个序列向右移动一位就好比L1

边覆盖

• 边覆盖（用边去覆盖点)

  设G=（V，E)是没有孤立顶点的简单图, E’⊆E,如果对任意的v∈V，都存在e∈E’，使得v是e的一个端点，则称E’为G的一个边覆盖

  E’的任何真子集都不是边覆盖,则称为极小边覆盖

  如果图G的边覆盖E’满足对于任何边覆盖E’‘，都有

  E’

  ≤

  E’’

  ,则称E’是G的一个最小边覆盖，其元素个数称作覆盖数，记作P（G）

注: (a)有孤立顶点的简单图不存在边覆盖

(b)极小边覆盖E’中任何一条边的两个端点不可能都与E’中的其他边关联

(c)明显有P（G) ≥

V

/2

(d)一个图中的极小边覆盖，最小边覆盖都不唯一

(e)最小边覆盖是极小，但极小不一定是最小

• 例子:

  (a)在任一简单图G(V,E)中,E都是边覆盖

  (b)任何完美匹配都是最小边覆盖

  (c)完全图Kn(n≥3)的边覆盖数为 ceiling(n/2)

  (d)完全二部图Km,n的支配数为max(m,n)

  (e)圈图Cn（n≥3）的边覆盖数为 ceiling(n/2)

  (f)轮图Wn(n≥3)的边覆盖数为 floor(n/2) + 1

• 最大匹配与最小边覆盖之间的关系
  • 定理1

    设G=(V,E)是没有孤立顶点的简单图,M为G的一个匹配，N为G的一个边覆盖,则|N| ≥ P(G)(最小边覆盖数) ≥ |V|/2 ≥ V(G)(最大匹配数) ≥ |M|； 且当等号成立时，M为G的一个完美匹配,N为G的一个最小边覆盖

（这个定理很显然，就不证啦） + 定理2

设G=(V,E)是没有孤立顶点的简单图,则有

(a)设M为G的一个最大匹配,对G中每一个M-非饱和顶点均取一条与其关联的边,组成集合N,则M∪N构成G的一个最小边覆盖，

图示如下:

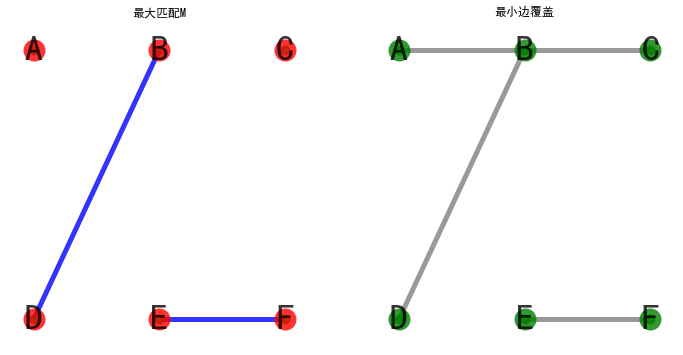
(b)设N为G的一个最小边覆盖,若N存在相邻的边，则移去其中一条,直至不存在相邻的边为止,构成的边集合M则为G的一个最大匹配

图示如下:

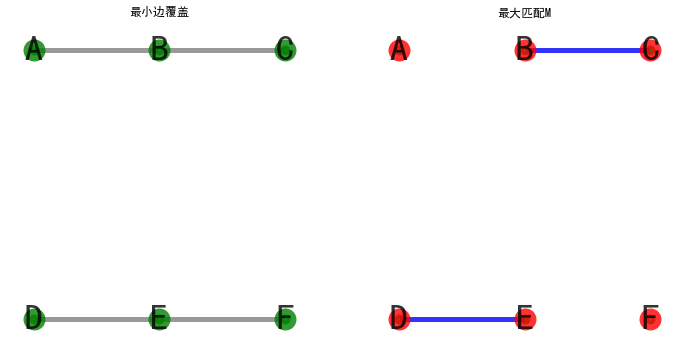
(c) P(G) + V(G) =

V

(三条一起证)证明:

(a)由于M为G的一个最大匹配,因此G由n-2 * V（G）个非饱和顶点，不可能有两个相邻的非饱和顶点，因此|N| = n-2 * V（G），|M∪N| = n-2 * V（G） + V(G) = n-V（G） 显然M∩N构成了G中的一个边覆盖，因此n-V（G）≥P（G）

(b)由于N是一个最小边覆盖，因此N中任何一条边的两个端点不可能都与其他边相关联。所以从N中移去边的时候，产生且只产生了M中的一个M-非饱和顶点。而最终M-非饱和顶点的个数 为n-2|M|， 故移去边的数目是n-2|M|（因为移去一个边就产生一个非饱和点）。得到|M| = |N| - （n-2|M|） => |N| = n - |M|； 又因为|N|是最小边覆盖：P（G）= |N| = n - |M| ≥ n - V(G)（因为V(G)(最大匹配数) ≥ |M|）

(c)由（a)可得 n-V（G）≥P（G）；由(b)可得P（G） ≥ n - V(G)； 所以 P（G） = n - V(G)；即P(G) + V(G) =

V

柯尼希给出：二部图中匹配数和最小点覆盖数的相等关系

• 引理

  假设K为没有孤立顶点的简单图G的任意一个点覆盖集，M为G的任意一个匹配，则

  M

  ≤

  K

  。 特别是V（G） ≤ β（G）(点覆盖数，用点去覆盖边)

证明: 因为一个顶点覆盖一条边, 而对于一个匹配,只需要与匹配数相同的点就能实现点覆盖， 那么剩余的每一个非饱和点都用一个点去覆盖;所以V（G） ≤ β（G）

• 推论

  假设K为没有孤立顶点的简单图G的任意一个点覆盖集，M为G的任意一个匹配， 若

  M

  =

  K

  ， 则M是一个最大匹配，K是一个最小覆盖

证明: 由

M

≤ V（G）≤ β（G）≤

K

即得 （第一个等号成立条件：最大匹配；第二个等号成立条件：引理：第三个等号成立条件：最小覆盖)

• 柯尼希-艾盖尔瓦里定理

  二部图中最大匹配的匹配数 = 最小点覆盖的覆盖数

证明:

假设M为最大匹配，V’为G的一个最小点覆盖集

（1） 由上面引理

M

≤

V’

（2） 令Xc = V’∩X， Yd = V’∩Y， C =

Xc

， d =

Yd

考虑顶点为Xc∪（Y-Yd）的G的导出子图G’，它也是二部图，其中存在使Xc中每个顶点饱和的匹配M1；

（反证法） 若存在S⊆Xc，

NG’(S)

<

S

(NG’(S)表示G’中与S相邻的点)

则（V’-S）∪NG’(S)同样构成了点覆盖集，但元素小于V’, 与V’的最小性矛盾

同理,顶点为（X-Xc）∪Yd的G的导出子图G’, 它也是二部图,其中存在使Yd中每个顶点饱和的匹配M2

易见 M1∪M2 也是G的一个匹配，于是

M

≥

M1∪M2

=

M1

+

M2

=

Xc

+

Yd

=

V’

再结合（1），可得

M

=

V’

• 由最大匹配构造最小点覆盖

①如果X中不存在M-非饱和顶点，则X本身就是一个最小点覆盖集

（如果x是孤立顶点，则不会出现在任何匹配和最小点覆盖中，因此不考虑所有孤立顶点）

②X中存在M-非饱和顶点， 考察所有从x开始的交错道路，记Y中所有x可以通过这些道路到达的顶点为集合Yx，并记 Y1 = ∪（x∈X） Yx

易见每个Y1中的元素都与M中唯一的一条边关联,记M中与Y1中的元素关联的边集合为M1，则	Y1	=	M1	，记X中与M-M1相关联的顶点集合为X1，则	X1	=	M	-	M1	；
明显有	Y1∪X1	=	Y1	+	X1	=	M

断言： Y1∪X1就是一个最小点覆盖

只需证明：Y1∪X1是一个点覆盖集即可，（’最小性’由最大匹配数决定）

（反证法）如果存在边uv，u∈X-X1，v∈Y-Y1，则由X1,Y1的构造方法可知:

或者u本身是M-非饱和点，经过uv可到达顶点v； 或者存在M-非饱和顶点x∈X，以x开始的某一条交错道路P可到达顶点u；这两者都能与v∈Y-Y1相矛盾；

二部图的匹配

(算法)最大权匹配(指派问题)

输入：赋权完全二部图 G = (X,Y,E)

输出: G的一个最大权匹配

在这里我主要用DFS来遍历所有组合然后选出最大的权匹配即可

• 具体题目描述 n个人干n项工作，第i个人干第j项工作能获得Cij单位收益, 要求把人跟工作匹配，收益总和最大

C = [[12,7,9,7,9],[8,9,6,6,6],[7,17,12,14,12],[15,14,6,6,10],[4,10,7,10,6]]

#%%最大权匹配(指派问题)
import copy
def template(matrix):  # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
    result = []  # 这个保存结果
    profit = 1e10
    def trace(path, choices):  # 递归函数
        '''
        path: dict 用于储存找到的零 key表示row values表示column
        choices: 矩阵matrix
        '''
        nonlocal result,profit
        if len(path) == len(matrix):  # 当path的长度等于输入的n时，结束算法，把结果加入结果列表
            # 计算profit
            temp = 0
            for row in path:
                temp += choices[row][path[row]]
            # 比较当前方案与此前最优方案
            if temp < profit:
                result = copy.deepcopy(path)
                profit = temp
            return

        for row in range(len(choices)):
            for column in range(len(choices)):
                    if row in path.keys():
                        continue
                    if column in path.values():  # 减枝操作(如果path里面有column,说名这一列已经有零了)
                        continue
                    path[row] = column  # 如果没有就把他加到目前的path中
                    trace(path, choices)  # 递归调用自身
                    path.popitem()  # 撤销最后一次的选择继续向前找答案

    trace({}, matrix)  # 调用函数trace
    return result
if __name__ == '__main__':
    C = [[12,7,9,7,9],
         [8,9,6,6,6],
         [7,17,12,14,12],
         [15,14,6,6,10],
         [4,10,7,10,6]]
    print(template(C))

可以看到结果输出的是{0: 2, 1: 4, 2: 1, 3: 0, 4: 3},带回C矩阵中发现,确实是最大的,再次说明了DFS是很有效且用途很广泛的算法

既然由最大权匹配当然也有最小权匹配

(算法)最小权匹配(指派问题)

输入：赋权完全二部图 G = (X,Y,E)

输出: G的一个最小权匹配

• 具体题目描述 n个人干n项工作，第i个人干第j项工作能消耗Cij单位时间, 要求把人跟工作匹配，时间耗费最小

C = [[12,7,9,7,9],[8,9,6,6,6],[7,17,12,14,12],[15,14,6,6,10],[4,10,7,10,6]]

#%%最小权匹配(指派问题)
def template(matrix):  # 主函数(设定他的目的是保证储存结果的result不会因为递归栈的关闭而丢失)
    result = []  # 这个保存结果
    profit = 1e10
    def trace(path, choices):  # 递归函数
        '''
        path: dict 用于储存找到的零 key表示row values表示column
        choices: 矩阵matrix
        '''
        nonlocal result,profit
        if len(path) == len(matrix):  # 当path的长度等于输入的n时，结束算法，把结果加入结果列表
            # 计算profit
            temp = 0
            for row in path:
                temp += choices[row][path[row]]
            # 比较当前方案与此前最优方案
            if temp < profit:
                result = copy.deepcopy(path)
                profit = temp
            return

        for row in range(len(choices)):
            for column in range(len(choices)):
                    if row in path.keys():
                        continue
                    if column in path.values():  # 减枝操作(如果path里面有column,说名这一列已经有零了)
                        continue
                    path[row] = column  # 如果没有就把他加到目前的path中
                    trace(path, choices)  # 递归调用自身
                    path.popitem()  # 撤销最后一次的选择继续向前找答案

    trace({}, matrix)  # 调用函数trace
    return result
if __name__ == '__main__':
    C = [[12,7,9,7,9],
         [8,9,6,6,6],
         [7,17,12,14,12],
         [15,14,6,6,10],
         [4,10,7,10,6]]
    print(template(C))

可以看到结果输出的是{0: 1, 1: 2, 2: 0, 3: 3, 4: 4}，带回C矩阵中发现,确实是最小的

细心的同学可能看出来了上面这个结果好像跟之前矩阵找零的那个结果一样,对的这两题用的矩阵都是同一个矩阵，只不过找零的那题的矩阵是用了Hungary算法处理过的

图的着色

• 图的着色

  对简单图G的每个顶点赋予一种颜色使得相邻的顶点颜色不同，称图G的一种点着色。对简单图G进行点着色所需的最少颜色数称为G的点色数，记为χ(G)

（注：对于n阶简单图，显然有χ(G)≤n）

• 边着色

  对简单图G的每条边赋予一种颜色，使得相邻边颜色不同,称为图G的一种边着色

• 面着色

  对无桥平面图图G的每个面赋予一种颜色,使得相邻的面颜色不同，称为图G的一种面着色

(利用对偶图，可以把平面图G的面着色问题转化为研究对偶图G’的点着色问题； 而通过下面的线图概念，也可以将图的边着色问题转化为点着色问题)

• 线图

  假设G是简单图，构造图L（G），G中的边和L（G）中的顶点一 一对应 ，如果G中的边e1和e2相邻，则L（G）中与e1和e2对应的两个顶点间连一条边，称L（G）是G的线图

• 例子： (a)χ(G)=1 当且仅当G是离散图

(b)χ(Kn) = n

(c)(圈图)χ(Cn) = 2, n是偶数时， χ(Cn) = 3，n是奇数时 （n≥3）

(d)(轮图)χ(Wn) = 3 ，n是偶数时， χ(Wn) = 4，n是奇数时 （n≥3）

(e)χ(Gn)=2 当且仅当G是二部图

而点着色问题是NP完全问题Non-deterministic Polynomial，尚不存在有效的方法求解

（给出近似算法）

• (算法)韦尔奇-鲍威尔算法 Welch_Powell（G）

输入: 简单图

输出：图G的一个着色方案

①将图中顶点按度数不增的方式排成排列

②使用一种新颜色对序列的一个顶点进行着色，并且按照序列次序，对与已着顶点不相邻的每一顶点着同样颜色，直至序列末尾。然后从序列中去掉已着色的顶点，得到一个新的序列

③对新序列重复步骤② ， 直至得到空序列

上代码!!!

#%%韦尔奇-鲍威尔算法
import networkx as nx
import matplotlib.pyplot as plt
from Vertex import Vertex
from Graph import Graph
import matplotlib as mpl

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.degree = 0   # 新增类属性(用于节点排序)
        self.color = 'white'  # 新增类属性(用于记录节点的颜色)

    # 重写类方法
    def addNeighbor(self, nbr, weight=0):   # 增加相邻边，默认weight为0
        '''
        input:
            nbr: Vertex object
            weight: int
        return:
            None
        '''
        self.connectedTo[nbr] = weight
        self.degree += 1

    # 新增类方法 (查看degree)
    def getDegree(self):
        return self.degree

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color
    
class colorGraph(Graph):
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

# 队列数据结构
class Queue():
    def __init__(self):
        self.queue = []

    def enqueue(self, item):
        self.queue.append(item)

    def dequeue(self):
        return self.queue.pop(0)

    def isEmpty(self):
        return self.queue == []

    def size(self):
        return len(self.queue)

    def __iter__(self):
        return iter(self.queue)

    # 查看队首元素
    def see(self):
        return self.queue[0]

class Solution():
    def createGraph(self, a_dict):
        graph = colorGraph()
        for i in a_dict:
            for j in a_dict[i]:
                graph.addEdge(i, j)
        return graph

    # 排序算法 -快速排序
    def quickSort(self, a_list):
        if len(a_list) <= 1:  # 有可能出现left或者right是空的情况
            return a_list
        else:
            mid = a_list[len(a_list)//2]
            left = []
            right = []
            a_list.remove(mid)
            for i in a_list:
                if i[1] > mid[1]:
                    right.append(i)
                else:
                    left.append(i)
            return self.quickSort(left) + [mid] + self.quickSort(right)

    def Welch_Powell(self, g):
        queue = Queue()
        Vertices_keys = g.getVertices()
        Vertices_obj = [g.getVertex(k) for k in Vertices_keys]
        # 用于储存顶点和他的degree
        Vertices_deg = [[i, i.getDegree()] for i in Vertices_obj]
        # 对Vertices_deg进行排序, 然后扔进队列里
        for i in self.quickSort(Vertices_deg)[::-1]:
            queue.enqueue(i[0])
        # 当队列非空
        color = 0  # 颜色标记
        # 已着色顶点
        color_done_vertex = []
        while not queue.isEmpty():
            # 对第一个点进行着色
            frist_vertex = queue.dequeue()
            frist_vertex.setColor(color)
            color_done_vertex.append(frist_vertex)
            for _ in range(queue.size()):
                # 如果color_done_vertex与i这个节点有连接
                Connections = []
                for k in color_done_vertex:
                    Connections += list(k.getConnections())
                if queue.see() in Connections:
                    # 将节点从队首加到队尾
                    queue.enqueue(queue.dequeue())
                else:
                    temp = queue.dequeue()
                    temp.setColor(color)
                    color_done_vertex.append(temp)
            color += 1
        # 输出结果
        result = []
        while Vertices_obj:
            temp_vertex = Vertices_obj.pop()
            result.append((temp_vertex.getId(), temp_vertex.getColor()))
            print(temp_vertex.getId(), ' 的颜色是:', temp_vertex.getColor())
        return result

if __name__ == '__main__':
    a_dict = {'a':['b', 'g', 'h'],
              'b':['a', 'd', 'g', 'h'],
              'c':['d', 'e'],
              'd':['b', 'c', 'f'],
              'e':['c', 'f'],
              'f':['d', 'e'],
              'g':['a', 'b', 'h'],
              'h':['a', 'b', 'g']}
    s = Solution()
    graph = s.createGraph(a_dict)
    result = s.Welch_Powell(graph)

    G = nx.Graph()
    for i in a_dict:
        for j in a_dict[i]:
            G.add_edge(i, j)
    
    color = list(mpl.colors.TABLEAU_COLORS.values())
    node_color = []
    for i in result:
        node_color.append(color[i[1]])
    plt.clf()
    pos = nx.spring_layout(G)
    nx.draw(G, pos, node_color=node_color, font_size= 35,with_labels=True)

结果如下:

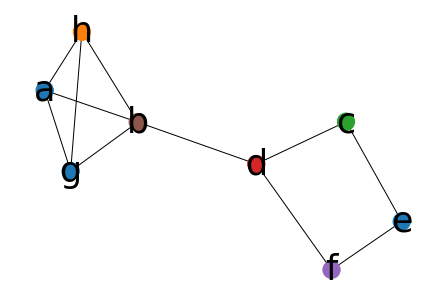
很明显这个不是最优解,把f可以换成棕色，c可以换成橙色，这样就用4种颜色来着色

之所以产生这样的问题，其一是：这个算法本身就是一种贪心策略的算法，难免会掉入局部最优

其次是这个算法的第一步是对顶点进行排序，排序的时候相同度数的顶点的顺序其实是不确定的，也会导致结果不优

网络与流

• 网络与流

  假设G=（V，E）是一个连通无重边且不包含自环的有向图，如果G中

  （1）只有一个入度为0的顶点，记之作为s，称为源

  （2）只有一个出度为0的顶点,记之作为t，称为汇

  （3）每条有向边e=（u，v）都存在一个非负权值Cuv，称作边的容量

  则称G是一个网络或流网络，也记作G=（V，E，s，t，C）

注：（问题转化)

①若存在重边，对重边求和作为一条边总容量

②自环的存在与否不影响问题的分析

③在实际应用中，还要考虑中转站的容量上限

④如果有多个源或者汇，那么新增两个顶点，S，T作为 源的源 和 汇的汇 ，并且将足够大的容量C0赋予这些新加的有向边（指的是S到多个源s的边，T到多个汇t的边）

• 前驱、后继

  假设顶点v∈V,定义v的前驱为pred（v) = {u

  （u，v）∈E}

  定义v的后继为secc（v)={u

  （u，v）∈E}

• 流（流量)

  若实值函数f: E→R满足

  （1）容量限制：对所有e=（u，v）∈E，有fuv = f（e） ≤Cuv

  （2）流量守恒：对所有顶点v∈V-{s,t}, ∑（u∈pred(v))fuv = ∑（u∈succ(v))fuv

  则称他是网络的一个容许流分布，或简称一个流，fuv称作边（u，v）上的流量，若e=（u，v）满足fuv = Cuv，则称e为饱和边

• 流入（出）量

  对所有顶点v∈V-{s}，定义f（ · ,v） = ∑（u∈pred(v))fuv，称作顶点v的总流入量

  对所有顶点u∈V-{t}，定义f（u ,· ） = ∑（v∈pred(u))fuv，称作顶点v的总流出量

  （为完整性考虑，补充定义f（ · ,s）= 0， f（t，· ）= 0

流量守恒表明：流在除了元和汇以外的各个顶点的总流入等于总流出量

• 最大流

  设f是网络图G的一个流，f（s，·）称作流f的流量，即源s的总流出量，记作

  f

  。若G的任意一个流f’都满足

  f

  ≥

  f’

  ，则称f是G的一个最大流

• S-T割（非常重要)

  在网络G = （V,E,s,t,c)中，任何一个满足s∈S，t∈T = V-S的顶点V的划分（S，T）称作一个S-T割，简称割

  一个S-T割的容量定义为 ∑（u∈S，v∈T，uv∈E）Cuv，记作Cuv（S，T）

  如果图G的S-T割使得任意一个G的S-T割（S’，T’）都有Cap（S，T）≤Cap（S’，T’）则称（S，T）是图G的一个最小S-T割，简称最小割

• 符号说明

  在网络G = （V,E,s,t,c）中，假设A、B都是V的非空子集,定义f（A，B） = ∑（u∈S，v∈T，uv∈E）fuv，即从A穿出进入B的边的总流量，定义C（A，B）= ∑（u∈A，v∈B，uv∈E）Cuv，即从A穿出进入B的边的总容量

• (定理)割流量 = 总流量

  假设G =（V,E,s,t,c）是一个网络，令f是一个流，（S，T）是一个S-T割，则通过该割的流量 = 由源s发出的流量；即f（S，T)-f（T,S） =

  f

  特别地，有f（·， t) =

  f

证明：（对

S

进行归纳证明）

①当S={s}的时候显然成立

②假设定理对于

S

＜k的时候成立；（这个{v，}后面的”,”是是显示问题）

当

S

= k时， 任取v∈S-{s，}，令S’= S-{v，}， T’ = T∪{v，}（这一步是把S中k个对象将为k-1个，然后可以用假设）

则由

S’

= k-1 可知f（S’，T’）-f（T’，S’）=

f

将顶点v添加到S’后，有

f（S，T）-F（S，T）

= （f（S’，T’）-f（S’，{v，}）+f（{v，}，T））-（f（T’，S’）-f（T，{v，}）+f（S’，{v，}））

= f（S’，T’） - f（T’，S’） + （f（{v，}，T） + f（{v，}，S’）- f（T，{v，}） - f（T，{v，}））

= f（S’，T’） - f（T’，S’） + f（v，·）- f（·，v）

= f（S’，T’） - f（T’，S’） =

f

• 最大流的上限由最小割决定

  设G是一个网络，令f是G的一个流，（S，T）是G的一个S-T割，则

  f

  ≤Cap（S，T）

证明： 由上面的定理

f	= f（S，T） - f（T，S）≤f（S，T）= ∑（u∈S，v∈T，uv∈E）fuv ≤ ∑（u∈S，v∈T，uv∈E）Cuv = Cap（S，T）

• 推论

  设G是一个网络，f是一个流，（S，T）是一个S-T割，则若

  f

  = Cap(S,T),则f是一个最大流且（S，T）是一个最小割

证明：假设f1是任意一个流，则由上面定理可得，

f1

≤

f

，则f是一个最大流

假设（S1,T1)是任意一个S-T割，则由上面定理，可得Cap（S，T）=

f

≤Cap（S1，T1），因此（S，T）是一个最小S-T割

（因此只要找到最小S-T割就能找到最大流）

• 剩余图

  假设网络G =（V,E,s,t,c）中有流f，则可如下定义G关于f的剩余图为Gf =（V,E,s,t,c’）

  （1）Gf的顶点集与G的顶点相同

  （2）Gf的边集合Ef有两类：{（u，v）	fuv<Cuv},称为前向边； {（u，v）	fvu>0},称为后向边；
  即Ef = {（u，v)	fuv0}

  (3)容量Cuv’= Cuv - fuv(if fuv<Cuv) or fvu (if fvu > 0)

(说白了就是把边反过来)

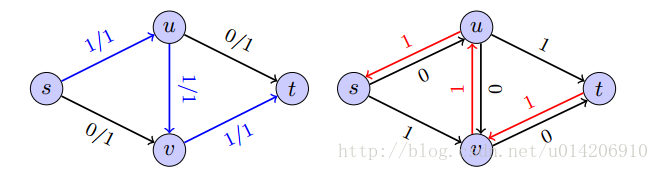
如图一个由流构造剩余图的例子：

• 可增广道路

  假设网络G =（V,E,s,t,c）中由流f，G关于f的剩余图中的简单s-t道路（就是由源s到汇t的道路）P称作可增广道路，定义bottleneck（P，f）为P所经过各边的最小流量（bottleneck意思是瓶颈）

  可以由增广道路P构造G的一个新流f’;

  当（u，v）是P中的前向边， fuv’ = fuv + bottleneck（P，f）

  当（u，v）是P中的后向边，fuv’ = fuv - bottleneck（P，f）

  其他情况时， fuv

可以验证函数f’满足容量条件和守恒条件：

（1）满足容量条件。对于不在道路P上的边而言，不产生任何变化

如果（u，v）是P中的前向边， fuv’ = fuv + bottleneck（P，f）≤fuv + Cuv’ = fuv + Cuv - fuv = Cuv；

如果（u，v）是P中的后向边， fuv’ = fuv - bottleneck（P，f）≤fuv≤ Cuv；

（2）满足守恒条件，对于不在道路P上的顶点而言，不产生任何变化

对于在P上的顶点v∈V-{s,t}，假设在道路P上与v关联的边是（u，v）和（v，w）

①如果（u，v）和（v，w）都是P中的前向边，则

f’（·，v） - f’（v,·） = (f(·，v) + bottleneck（P，f）) - （f（v，·） + bottleneck（P，f））=f(·，v) - f（v，·） = 0

②如果（u，v）和（v，w）都是P中的后向边，则

f’（·，v） - f’（v,·） = (f(·，v) - bottleneck（P，f）) - （f（v，·） - bottleneck（P，f））=f(·，v) - f（v，·） = 0

③如果（u，v）是P中的前向边， （v，w）是P中的后向边，则

f’（·，v） - f’（v,·） = (f(·，v) - bottleneck（P，f）+ bottleneck（P，f）) - f（v，·）=f(·，v) - f（v，·） = 0

④如果（u，v）是P中的后向边， （v，w）是P中的前向边，则

f’（·，v） - f’（v,·） = f(·，v) - （f（v，·）- bottleneck（P，f）+ bottleneck（P，f）)=f(·，v) - f（v，·） = 0

而且

f’

= f’（s,·） = f（s,·） + bottleneck（P，f） > f（s,·） =

f

,即流的流量得以提升

• 最大流，最小割定理

  假设f是网络G =（V,E,s,t,c）的一个流，则一下陈述等价

  (a)f是一个最大流

  (b)当且f的剩余图中不存在增广道路

  (c)存在G的一个S-t割（S，T）使得

  f

  = Cap（S，T）

证明：(a)=>(b)

如果当前关于f的剩余图中存在可增广道路，则可以通过这条道路扩大流，与f是最大流矛盾

(b)=>(c)

假设f是不存在可增广道路的流，设S是在当前剩余图由s可达的顶点之集合，显然s∈S，且t∉S，否则存在增广道路；

令T = V - S，假设u∈S，v∈T，若（u，v）∈E，则必有fuv = Cuv，否则（u，v）∈Ef，v也由s可达，与S的定义矛盾；

若（v,u）∈E，则必然有fvu=0，否则（u，v）∈Ef，v也由s可达，与S的定义矛盾

(c)=>(a) ：由上面的推论可得

(算法)Ford-Fulkerson（G) (最大流最小割算法)

输入： 网络G =（V,E,s,t,c）

输出： G的一个最大流f

①初始流量选为0流量，即对所有边uv，fuv←0

②构造G关于f的剩余图Gf

③若Gf中存在增广道路P，则按照前述方法构造由增广道路P，构造G的一个新流f’,f←f’，转到②

否则输出f

(通俗来说，就是在图中随便找一条路，再把路反过来，再找一条路，再把路反过来，往复这个过程直达找不到路就是最大流了)

实现算法过程注意几点：（是我再写代码中的出来的关键）

因为f永远是正的，跟初始边的方向是同向的，所以f不需要再建一个图，直接把f并入边的属性即可cost=[f,c]，所以图的数据结构要修改

增广道路的搜寻方法多种多样，可以用前面的DFS(固定起始点s，当path的最后一个元素是t时输出path即可)，我这里采用BFS（广度优先搜素，详细的可以继续往后看，会说BFS）

剩余图也用同一个数据结构，但是边属性只有一个C,cost=c

接下来，还是看代码！！！冲！！！

#%%Ford-Fulkerson算法求解最大流问题
from Vertex import Vertex # 导入Vertex
from Graph import Graph  # 导入之前实现的Graph
import sys

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.color = 'white'  # 新增类属性(用于记录节点是否被走过)
        self.dist = sys.maxsize  # 新增类属性(用于记录strat到这个顶点的距离)初始化为无穷大
        self.pred = None  # 顶点的前驱 BFS需要

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

    # 新增类方法, 设置节点前驱
    def setPred(self, p):
        self.pred = p

    # 新增类方法, 查看节点前驱
    def getPred(self):  # 这个前驱节点主要用于追溯，是记录离起始节点最短路径上
        return self.pred    # 该节点的前一个节点是谁

    # 新增类方法, 设置节点距离
    def setDistance(self, d):
        self.dist = d

    # 新增类方法, 查看节点距离
    def getDistance(self):
        return self.dist

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        if key in self.vertList:
            return
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

# %广度优先算法（先从距离为1开始搜索节点，搜索完所有距离为k才搜索距离为k+1）
'''
为了跟踪顶点的加入过程，并避免重复顶点，要为顶点增加三个属性
    距离distance:从起始顶点到此顶点路径长度
    前驱顶点predecessor:可反向追随到起点
    颜色color：标识了此顶点是尚未发现（白色）,已经发现（灰色）,还是已经完成探索（黑色）
还需用一个队列Queue来对已发现的顶点进行排列
    决定下一个要探索的顶点（队首顶点）

BFS算法过程
    从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None，
    加入队列，接下来是个循环迭代过程：
        从队首取出一个顶点作为当前顶点；遍历当前顶点的邻接顶点，如果是尚未发现的白
        色顶点，则将其颜色改为灰色（已发现），距离增加1，前驱顶点为当前顶点，加入到队列中
    遍历完成后，将当前顶点设置为黑色（已探索过），循环回到步骤1的队首取当前顶点
'''

# 队列 -- 也是BFS需要的
class Queue:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def enqueue(self, items):   # 往队列加入数据
        self.items.insert(0, items)

    def dequeue(self):
        return self.items.pop()

    def size(self):
        return len(self.items)

class max_flow_graph():
    # 创建图和初始化流f
    # 注意图中的cost由[flow, cost] 组成 前者表示流量 后者表示容量
    # 既可以传入字典也能传入邻接矩阵
    def createGraph_f(self, g_dict=None, g_matrix=None):
        '''
        input: g_dict(邻接表) or g_matrix(邻接矩阵)
        output: directgraph(有向图)
        '''
        graph = New_Graph()
        # f = Graph()
        if g_dict:
            for from_key in g_dict:
                for to_key in g_dict[from_key]:
                    # 这里就是注意提到的f跟着c走所以原图的c是[f,c],这个很重要
                    graph.addEdge(from_key, to_key[0], [0, to_key[1]])

        elif g_matrix:
            # 先给顶点起个名字
            name = [str(i) for i in range(1, len(g_matrix)+1)]
            for i, from_key in enumerate(name):
                for j, to_key in enumerate(name):
                    if g_matrix[i][j] != float('inf'):
                        graph.addEdge(from_key, to_key, [0,g_matrix[i][j]])
        return graph

    # 得到简单的s-t道路P
    def BFS(self, gf, start, end):   # g是图，start是起始的节点
        '''
        g: Gf 剩余图
        start: key
        end: key
        return: p 以节点为元素的道路列表
        '''
        start.setDistance(0)  # 距离
        start.setPred(None)  # 前驱节点
        vertQueue = Queue()   # 队列
        vertQueue.enqueue(start)  # 把起始节点加入图中
        while vertQueue.size() > 0:   # 当搜索完所有节点时，队列会变成空的
            currentVert = vertQueue.dequeue()  # 取队首作为当前顶点
            for nbr in currentVert.getConnections():  # 遍历临接顶点
                if (nbr.getColor() == 'white'):   # 当邻接顶点是灰色的时候
                    nbr.setColor('gray')
                    nbr.setDistance(currentVert.getDistance() + 1)
                    nbr.setPred(currentVert)
                    vertQueue.enqueue(nbr)
            currentVert.setColor('balck')
        P = []
        P.append(end)
        while end.getPred():
            end = end.getPred()
            P.append(end)
        return P[::-1]

    # 由原图构造剩余图
    def create_remain_graph(self, g):
        '''
        input: g有向图(包含flow流量和cost容量)
        output: gf剩余图(就是把flow的方法反过来的一个图)
        '''
        # 剩余图gf的边只有一个属性就是cost
        gf = New_Graph()
        # 获得顶点集
        verlist = g.vertList
        for i in verlist:
            from_key = verlist[i]
            gf.addVertex(from_key.getId())
            for to_key in from_key.getConnections():
                gf.addVertex(to_key.getId())
                f = from_key.getWeight(to_key)[0]  # f表示流
                c = from_key.getWeight(to_key)[1]  # c表示容量
                # 前向边
                if f <  c:
                    c_new = c - f
                    gf.addEdge(from_key.getId(), to_key.getId(), c_new)
                # 后向边
                if f > 0:
                    gf.addEdge(to_key.getId(), from_key.getId(), f)
        return gf

    def print_flow(self, g):
        '''
        input: g 带流的图
        output: flow_matrix
        '''
        result = [[0]*len(g) for _ in range(len(g))]
        for i in range(1, len(g)):
            from_key = str(i)
            for j in range(i+1, len(g)+1):
                to_key = str(j)
                from_Vertex = g.getVertex(from_key)
                to_Vertex = g.getVertex(to_key)
                try:
                    result[i-1][j-1] = from_Vertex.getWeight(to_Vertex)[0]
                except:
                    pass
        return result
                
    def Ford_Fulkerson(self, g):
        '''
        算法主流程:
            1.初始化流为0 (f<--0)(我把这步放到createGraph中了)
            2.构造G关于f的剩余图gf
            3.若gf中存在增广道路P, 则由增广道路P构造G的一个新流f’
              f <-- f' 转步骤2
              否则输出f

        Parameters
        ----------
        g : graph
            由createGraph_f创建的图.
            
        Returns
        -------
        choice matrix
            流量方案的选择(每一行表示一个流出点, 每一列表示一个流入点).

        '''
        # 构造g关于f的剩余图Gf
        gf = self.create_remain_graph(g)
        # 求出Gf的增广道路
        P = self.BFS(gf, gf.getVertex('1'), gf.getVertex(str(len(g))))
        # 若存在增广道路 则由增广道路构造G的一个新流f
        while len(P)>1:
            # 计算增广路中的bottleneck
            bottleneck = 1e5
            for i in range(len(P)-1):
                if P[i].getWeight(P[i+1]) < bottleneck:
                    bottleneck = P[i].getWeight(P[i+1])
            # 更新f
            for i in range(len(P)-1):
                u_name = P[i].getId()
                v_name = P[i+1].getId()
                u = g.vertList[u_name]
                v = g.vertList[v_name]
                c = u.getWeight(v)
                # 如果(u,v)是g中的正向边
                if v in u.getConnections():
                    c[0] += bottleneck
                elif u in v.getConnections():
                    c[0] -= bottleneck
                # 流一定是正向的，只有剩余图的边有可能是反向的
                g.addEdge(u_name, v_name, c)
            # 更新gf
            gf = self.create_remain_graph(g)
            # 求出Gf的增广道路
            P = self.BFS(gf, gf.getVertex('1'), gf.getVertex(str(len(g))))
        return self.print_flow(g)

if __name__ == '__main__':
    g_dict ={'1':[['2', 10], ['3', 10]],
             '2':[['3', 2], ['4', 4], ['5', 8]],
             '3':[['5', 9]],
             '4':[['6', 10]],
             '5':[['4', 6], ['6', 10]]}
    s = max_flow_graph()
    g = s.createGraph_f(g_dict)
    print(s.Ford_Fulkerson(g))

(注：如果各边的容量都是整数，则每次f←f‘的更新都使得流的值至少增加1，因此算法至多再∑（v∈suss(s）Csv次结束，如果各边的容量是一般实数，那么该算法永远运行下去)

• 网络最大流的应用

  可以将二部图的匹配问题转化为网络流图

  步骤：（1）将原图所有无向边改为有向边，由X中顶点指向Y中顶点

  （2）添加一个超源顶点S和一个超汇顶点T

  （3）添加S到X中每个顶点的有向边，添加Y中每个顶点到T的有向边

  （4）所有有向边的容量都设置为1

所得的图称作匹配网络，显然二部图中的最大匹配对应匹配网络的最大流。（看到这里是不是豁然开朗了，原来网上说的二部图的最大匹配算法的原理是这样）

我的离散数学的图论笔记就到此为止了！！，如果你也是一个证明一个证明看下来，一行代码一行代码地敲下来的话，你已经很强啦！！！

接下来是一些算法的加餐！！继续冲 ！！！！

加餐部分

加餐第一题： 骑士周游问题DFS实现

• 题目：

  考虑国际象棋棋盘上某个位置的一只马，它是否可能只走63步，正好走过除起点外的其他63个位置各一次？如果有一种这样的走法，则称所走的这条路线为一条马的周游路线。试设计一个算法找出这样一条马的周游路线。

此题实际上是一个汉密尔顿通路问题，可以描述为：

在一个8×8的方格棋盘中，按照国际象棋中马的行走规则从棋盘上的某一方格出发，开始在棋盘上周游，如果能不重复地走遍棋盘上的每一个方格， 这样的一条周游路线在数学上被称为国际象棋盘上马的哈密尔顿链。请你设计一个程序，从键盘输入一个起始方格的坐标，由计算机自动寻找并打印 出国际象棋盘上马的哈密尔顿链。

算法很经典不过多解释了，但在实现的过程中用了一个启发式的算法Warnsdorff算法，目的只是加快DFS过程

• 骑士周游问题详解–陈斌老师（北大数据结构）

话不多说，上代码！！！

#%%骑士周游问题
from Vertex import Vertex # 导入Vertex
from Graph import Graph  # 导入之前实现的Graph

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.color = 'white'  # 新增类属性(用于记录节点是否被走过)

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

class Solution(object):
    # 构造图
    def knightGraph(self, bdSize):
        ktGraph = New_Graph()
        for row in range(bdSize):
            for col in range(bdSize):
                index = bdSize * row + col  # 当前节点索引(key)
                newPositions = self.genLegalMoves(row, col, bdSize)  # 下一个节点的集合
                for i in newPositions:
                    index_next = bdSize*i[0]+i[1]
                    ktGraph.addEdge(index, index_next, 1)
        return ktGraph

    # 判断马的走法是否合法
    def genLegalMoves(self, x, y, bdSize):
        newMoves = []
        # 马的走棋规则
        moveOffsets = [(-1, -2), (-1, 2), (-2, -1), (-2, 1),
                       (1, -2), (1, 2), (2, -1), (2, 1)]
        for i in moveOffsets:
            newX = x + i[0]
            newY = y + i[1]
            if self.legalCoord(newX, bdSize) and self.legalCoord(newY, bdSize):
                newMoves.append((newX, newY))
        return newMoves

    def legalCoord(self, x, bdSize):   # 查看落点是否越界
        if x >= 0 and x < bdSize:
            return True
        else:
            return False

    # 深度优先搜索
    def DFS(self, g, start):
        result = []

        # 回溯
        def trace(path, g, start):   # path是探索的路径 g是图，start是起始的节点
            start.setColor('gray')  # 将正在探索的节点设置为灰色
            path.append(start)
            if len(path) == 64:   # 64是总的目标（走完棋盘）
                result.append(list(path))
                return
            else:
                for i in list(start.getConnections()):
                    if i.getColor() == 'white':
                        trace(path, g, i)
                        path.pop()
                        i.setColor('white')

        trace([], g, start)
        return result

    # 回溯改进Warnsdorff算法
    # 将strat 的合法移动目标棋盘格排序为：具有最少合法移动目标的格子优先搜索
    # def Warnsdorff(g, start):

    # Warnsdorff算法
    def Warnsdorff(self, path, g, start):   # path是探索的路径 g是图，start是起始的节点
        start.setColor('gray')  # 将正在探索的节点设置为灰色
        path.append(start)
        temp_choice = list(self.orderByAvail(start))
        for i in temp_choice:
            if i.getColor() == 'white':
                self.Warnsdorff(path, g, i)
                if len(path) == 64:   # 64是总的目标（走完棋盘）(这与完全遍历有区别)
                    return path  # 完全遍历的判断语句就在函数前端，这个只要找到一个就行
                path.pop()
                i.setColor('white')

    # 这个函数的目的是把要探索的节点按照走的先后次序进行排序（按照下下步选择少的排在前面）
    # 相当于先验知识（启发式算法）
    def orderByAvail(self, start):
        reslist = []
        for i in start.getConnections():
            if i.getColor() == 'white':
                c = 0
                for j in i.getConnections():
                    if j.getColor() == 'white':
                        c += 1
                reslist.append((c, i))
        reslist.sort(key=lambda x: x[0])
        return [y[1] for y in reslist]

        # trace1([], g, start)
        # return result


if __name__ == '__main__':
    s = Solution()
    g = s.knightGraph(8)
    path = s.Warnsdorff([], g, g.getVertex(0))
    for i in path:
        print(i.getId(), end=' ')

加餐第二题： 词梯问题BFS实现

• 题目：

  从一个单词演变到另一个单词，其中的过程可以经过多个中间单词。 要求是相邻两个单词之间差异只能是1个字母

• 从FOOL到SAGE的过程

注意的地方：

图结构的构建有点复杂，主要思想就是构建词梯桶，把两个相差一个字符的单词构建一条边

然后就是BFS的实现了

广度优先算法（先从距离为1开始搜索节点，搜索完所有距离为k才搜索距离为k+1）

(图的数据结构修改) 为了跟踪顶点的加入过程，并避免重复顶点，要为顶点增加三个属性 距离distance:从起始顶点到此顶点路径长度 前驱顶点predecessor:可反向追随到起点 颜色color：标识了此顶点是尚未发现（白色）,已经发现（灰色）,还是已经完成探索（黑色）

(新加队列数据结构) 还需用一个队列Queue来对已发现的顶点进行排列 决定下一个要探索的顶点（队首顶点）

BFS算法过程 从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None， 加入队列，接下来是个循环迭代过程：

从队首取出一个顶点作为当前顶点；遍历当前顶点的邻接顶点，如果是尚未发现的白色顶点，则将其颜色改为灰色（已发现），距离增加1，前驱顶点为当前顶点，加入到队列中

遍历完成后，将当前顶点设置为黑色（已探索过），循环回到步骤1的队首取当前顶点

• 词梯问题详解–陈斌老师（北大数据结构）

话不多说，上代码！！！

#%% 词梯问题BFS算法
from Vertex import Vertex # 导入Vertex
from Graph import Graph  # 导入之前实现的Graph
import sys

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.color = 'white'  # 新增类属性(用于记录节点是否被走过)
        self.dist = sys.maxsize  # 新增类属性(用于记录strat到这个顶点的距离)初始化为无穷大
        self.pred = None  # 顶点的前驱 BFS需要

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

    # 新增类方法, 设置节点前驱
    def setPred(self, p):
        self.pred = p

    # 新增类方法, 查看节点前驱
    def getPred(self):  # 这个前驱节点主要用于追溯，是记录离起始节点最短路径上
        return self.pred    # 该节点的前一个节点是谁

    # 新增类方法, 设置节点距离
    def setDistance(self, d):
        self.dist = d

    # 新增类方法, 查看节点距离
    def getDistance(self):
        return self.dist

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        if key in self.vertList:
            return
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

# %词梯问题:采用字典建立桶（每个桶有三个字母是相同的  比如head,lead,read
# 那么每个词梯桶内部所有单词都组成一个无向且边为1的图


def buildGraph(wordfile):
    d = {}
    g = New_Graph()
    wfile = open(wordfile, 'r')
    # 创建桶，每个桶中只有一个字母是不同的
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):   # 每一个单词都可以属于4个桶
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    # 在桶内部建立图
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1, word2)
    return g


# %广度优先算法（先从距离为1开始搜索节点，搜索完所有距离为k才搜索距离为k+1）
'''
为了跟踪顶点的加入过程，并避免重复顶点，要为顶点增加三个属性
    距离distance:从起始顶点到此顶点路径长度
    前驱顶点predecessor:可反向追随到起点
    颜色color：标识了此顶点是尚未发现（白色）,已经发现（灰色）,还是已经完成探索（黑色）
还需用一个队列Queue来对已发现的顶点进行排列
    决定下一个要探索的顶点（队首顶点）

BFS算法过程
    从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None，
    加入队列，接下来是个循环迭代过程：
        从队首取出一个顶点作为当前顶点；遍历当前顶点的邻接顶点，如果是尚未发现的白
        色顶点，则将其颜色改为灰色（已发现），距离增加1，前驱顶点为当前顶点，加入到队列中
    遍历完成后，将当前顶点设置为黑色（已探索过），循环回到步骤1的队首取当前顶点
'''


class Queue:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def enqueue(self, items):   # 往队列加入数据
        self.items.insert(0, items)

    def dequeue(self):
        return self.items.pop()

    def size(self):
        return len(self.items)


def BFS(g, start):   # g是图，start是起始的节点
    start.setDistance(0)  # 距离
    start.setPred(None)  # 前驱节点
    vertQueue = Queue()   # 队列
    vertQueue.enqueue(start)  # 把起始节点加入图中
    while vertQueue.size() > 0:   # 当搜索完所有节点时，队列会变成空的
        currentVert = vertQueue.dequeue()  # 取队首作为当前顶点
        for nbr in currentVert.getConnections():  # 遍历临接顶点
            if (nbr.getColor() == 'white'):   # 当邻接顶点是灰色的时候
                nbr.setColor('gray')
                nbr.setDistance(currentVert.getDistance() + 1)
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
        currentVert.setColor('balck')


def traverse(y):
    x = y
    while (x.getPred()):
        print(x.getId())
        x = x.getPred()
    # print(x.getPred())


if __name__ == '__main__':
    wordgraph = buildGraph('fourletterwords.txt')
    BFS(wordgraph, wordgraph.getVertex('FOOL'))
    traverse(wordgraph.getVertex('SAGE'))
    print('FOOL')

看到结果输出的与上图不一致，但是经过的顶点的数量是相同的，都是最短路径，所以OK！！！

加餐第三题： 强连通分支（kosaraju算法）

关于强连通分支，前面有做过铺垫，找强连通分支有很多算法，这里将一个好理解的算法kosaraju算法，

• 算法流程：

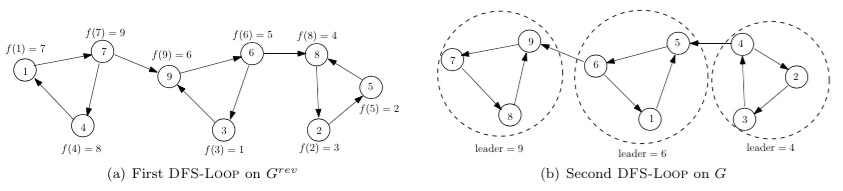
  强连通分量分解可以通过两次简单的DFS实现。第一次DFS时，选取任意顶点作为起点，遍历所有尚未访问过的顶点，并在回溯前给顶点标号(post order，后序遍历)。对剩余的未访问过的顶点，不断重复上述过程。

  完成标号后，越接近图的尾部(搜索树的叶子)，顶点的标号越小。第二次DFS时，先将所有边反向，然后以标号最大的顶点为起点进行DFS。这样DFS所遍历的顶点集合就构成了一个强连通分量。之后，只要还有尚未访问的顶点，就从中选取标号最大的顶点不断重复上述过程。

附上源视频链接

强连通分支（kosaraju算法）–陈斌老师（北大数据结构）

但是视频中可没有代码喔！！

那pd的nb之处还是展现出来了喔！！

话不多说，上代码！！！

# %%通用的深度优先搜索(kosaraju算法)
import sys


class Vertex:
    def __init__(self, key):
        self.id = key
        self.connectedTo = {}
        self.color = 'white'
        self.dist = sys.maxsize  # 无穷大
        self.pred = None
        self.disc = 0   # 发现时间
        self.fin = 0  # 结束时间

    def addNeighbor(self, nbr, weight=0):   # 增加相邻边，
        self.connectedTo[nbr] = weight

    def __str__(self):   # 显示设置
        return str(self.id) + 'connectTo:' + \
               str([x.id for x in self.connectedTo])

    def getConnections(self):   # 获得相邻节点
        return self.connectedTo.keys()

    def getId(self):   # 获得节点名称
        return self.id

    def getWeight(self, nbr):   # 获得相邻边数据
        return self.connectedTo[nbr]

    def setColor(self, color):
        self.color = color

    def getColor(self):
        return self.color

    def setPred(self, p):
        self.pred = p

    def getPred(self):  # 这个前驱节点主要用于追溯，是记录离起始节点最短路径上
        return self.pred    # 该节点的前一个节点是谁

    def setDistance(self, d):
        self.dist = d

    def getDistance(self):
        return self.dist

    def setDiscovery(self, dtime):
        self.disc = dtime

    def setFinish(self, ftime):
        self.fin = ftime

    def getFinish(self):
        return self.fin

    def getDiscovery(self):  # 设置发现时间
        return self.disc


class DFSGraph:
    def __init__(self):
        self.vertList = {}  # 这个虽然叫list但是实质上是字典
        self.numVertices = 0
        self.time = 0   # DFS图新增time 用于记录执行步骤

    def addVertex(self, key):   # 增加节点
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

    def getVertex(self, key):   # 通过key获取节点信息
        if key in self.vertList:
            return self.vertList[key]
        else:
            return None

    def __contains__(self, n):  # 判断节点在不在图中
        return n in self.vertList

    def addEdge(self, from_key, to_key, cost=1):    # 新增边
        if from_key not in self.vertList:      # 不再图中的顶点先添加
            self.addVertex(from_key)
        if to_key not in self.vertList:
            self.addVertex(to_key)
        # 调用起始顶点的方法添加邻边
        self.vertList[from_key].addNeighbor(self.vertList[to_key], cost)

    def getVertices(self):   # 获取所有顶点的名称
        return self.vertList.keys()

    def __iter__(self):  # 迭代取出
        return iter(self.vertList.values())

    def dfs(self):
        for v in self:
            v.setColor('white')   # 先将所有节点设为白色
            v.setPred(-1)

        for v in self:
            if v.getColor() == 'white':
                self.dfsvisit(v)  # 如果还有未包括的顶点,则建立森林

    def dfsvisit(self, stratVertex):
        stratVertex.setColor('gray')
        self.time += 1   # 记录步数
        stratVertex.setDiscovery(self.time)

        for v in stratVertex.getConnections():
            if v.getColor() == 'white':
                v.setPred(stratVertex)   # 把下一个节点的前驱节点设为当前节点
                self.dfsvisit(v)  # 递归调用自己
        stratVertex.setColor('black')  # 把当前节点设为黑色
        self.time += 1   # 设为黑色表示往回走了，所以步数加一
        stratVertex.setFinish(self.time)

    def kosaraju(self):  # kosaraju划分强连通分支
        self.dfs()  # 第一步调用DFS，得到节点的Finish_time
        # 第二步将图转置
        self.transposformed()  # 将图转置
        # 对转置的图调用DFS,但不能直接调用
        num = self.numVertices
        max_finish = 0
        while num > 0:
            for v in self:
                # 得到最大的Finish_time
                if v.getColor() == 'black' and v.fin >= max_finish:
                    max_finish = v.fin

            for v in self:
                # 按照Finish_time从大到小组成深度优先森林
                if v.fin == max_finish:
                    self.kosaraju_dfsvisit(v)
                    print('其中一个强联通分支是:')
                    for v in self:
                        if v.getColor() == 'gray':  # 将灰色的都返回
                            print(v.getId(), end=' ')
                            v.setColor('white')  # 将颜色设为白色
                            num -= 1   # 记录还剩多少节点
            max_finish = 0

    def transposformed(self):
        Edge_tuples = []  # 里面装 某节点-指向->相邻节点和相邻边
        for v1 in self:  # 把所有节点取出来
            for v2 in self:  # 两两交换边
                if v2 in v1.getConnections():
                    Edge_tuples.append((v1, v2, v1.getWeight(v2)))
            v1.connectedTo = {}  # 把v1的全部变成空
        for v3 in Edge_tuples:
            current_Vertex = v3[1]  # current_Vertex 是原本被指向的节点
            current_Vertex.addNeighbor(v3[0], v3[2])

    def kosaraju_dfsvisit(self, stratVertex):
        # 写一个专门用于kosaraju逆序的dfs
        stratVertex.setColor('gray')  # 把color从黑色转为灰色
        for v in stratVertex.getConnections():
            if v.getColor() == 'black':
                v.setPred(stratVertex)   # 把下一个节点的前驱节点设为当前节点
                self.kosaraju_dfsvisit(v)  # 递归调用自己


if __name__ == '__main__':
    g = DFSGraph()
    g.addEdge('A', 'B')
    g.addEdge('B', 'E')
    g.addEdge('B', 'C')
    g.addEdge('C', 'F')
    g.addEdge('E', 'A')
    g.addEdge('E', 'D')
    g.addEdge('D', 'G')
    g.addEdge('D', 'B')
    g.addEdge('G', 'E')
    g.addEdge('F', 'H')
    g.addEdge('H', 'I')
    g.addEdge('I', 'F')
    g.kosaraju()

正确结果：如图

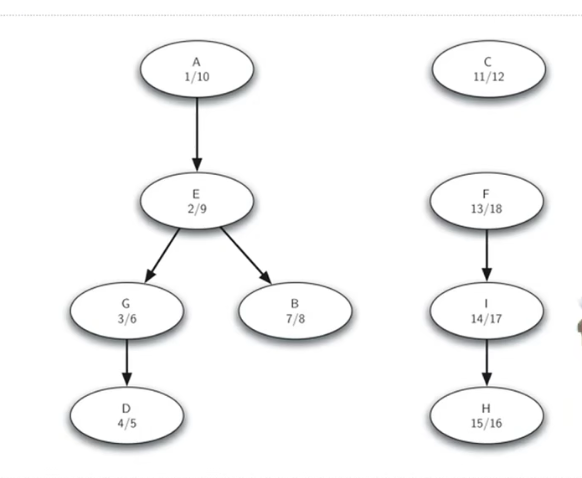
可以看到我们的结果与正确结果一致，OK！！！！

加餐第四题： 图的最短路径算法（Dijkstra算法）+ prim最小生成树

对于最短路径我们当然可以用DFS或者BFS来找到，但是Dijkstra算法也是一个很经典的算法

背景介绍在这里

图的最短路径算法–陈斌老师（北大数据结构）

话不多说，上代码！！！

# %%图的最短路径算法（Dijkstra算法）无法处理权值为负的情况

import sys
import numpy as np


class Binheap():
    def __init__(self):
        self.heaplist = [(0, 0)]   # 专门用于Dijkstra算法，第一个是节点第二个是数值
        # 因为要利用完全二叉树的性质，为了方便计算，把第0个位置设成0，不用他
        '''
        完全二叉树的特性  如果某个节点的下标为i
        parent = i//2
        left = 2*i
        right = 2*i +1
        '''
        self.currentSize = 0

    def perUp(self, i):
        while i//2 > 0:
            # 如果子节点比父节点要小，就交换他们的位置
            if self.heaplist[i][1] < self.heaplist[i//2][1]:
                self.heaplist[i], self.heaplist[i//2] =\
                                        self.heaplist[i//2], self.heaplist[i]
            i = i//2

    def insert(self, k):
        self.heaplist.append(k)
        self.currentSize += 1
        self.perUp(self.currentSize)

    def delMin(self):
        # 删掉最小的那个就是删掉了根节点，为了不破坏heaplist
        # 需要把最后一个节点进行下沉，下沉路径的选择，选择子节点中小的那个进行交换
        # 先把最后一个与第一个交换顺序
        self.heaplist[1], self.heaplist[-1] =\
                                    self.heaplist[-1], self.heaplist[1]
        self.currentSize -= 1
        self.perDown(1)
        return self.heaplist.pop()

    def minChild(self, i):
        if i*2+1 > self.currentSize:
            return 2*i
        else:
            if self.heaplist[2*i][1] < self.heaplist[2*i+1][1]:
                return 2*i
            else:
                return 2*i+1

    def perDown(self, i):  # 下沉方法
        while 2*i <= self.currentSize:  # 只有子节点就比较
            min_ind = self.minChild(i)
            if self.heaplist[i][1] > self.heaplist[min_ind][1]:
                # 如果当前节点比子节点中小的要大就交换
                self.heaplist[i], self.heaplist[min_ind] =\
                                self.heaplist[min_ind], self.heaplist[i]
                i = min_ind
            else:
                break  # 如果当前节点是最小的就退出循环

    def findMin(self):
        return self.heaplist[1]

    def isEmpty(self):
        return self.heaplist == [(0, 0)]

    def size(self):
        return self.currentSize

    def buildHeap(self, alist):  # 这个alist里面装的元素是元组
        # 将列表变为二叉堆
        # 采用下沉法 算法复杂度O(N)  如果一个一个插入的话，算法复杂的将会是O(nlgn)
        # 自下而上的下沉（先下沉最底层的父节点）
        i = len(alist)//2
        self.currentSize = len(alist)
        self.heaplist = [(0, 0)] + alist
        while i > 0:
            self.perDown(i)
            i -= 1
        return self.heaplist

    def __iter__(self):
        for item in self.heaplist[1:]:
            yield item

    def __contains__(self, n):    # 判断节点是否在优先队列内（专门为prim写的）
        return n in [v[0] for v in self.heaplist]


class Vertex:
    def __init__(self, key):
        self.id = key
        self.connectedTo = {}
        self.color = 'white'  # 为了解决词梯问题的
        self.dist = sys.maxsize  # 无穷大
        self.pred = None

    def addNeighbor(self, nbr, weight=0):   # 增加相邻边，
        self.connectedTo[nbr] = weight   # 这个nbr是一个节点对象，不是名称

    def __str__(self):   # 显示设置
        return str(self.id) + 'connectTo:' + \
               str([x.id for x in self.connectedTo])

    def getConnections(self):   # 获得相邻节点
        return self.connectedTo.keys()

    def getId(self):   # 获得节点名称
        return self.id

    def getWeight(self, nbr):   # 获得相邻边数据
        return self.connectedTo[nbr]

    def setColor(self, color):
        self.color = color

    def getColor(self):
        return self.color

    def setPred(self, p):
        self.pred = p

    def getPred(self):  # 这个前驱节点主要用于追溯，是记录离起始节点最短路径上
        return self.pred    # 该节点的前一个节点是谁

    def setDistance(self, d):
        self.dist = d

    def getDistance(self):
        return self.dist


class DIJKSTRAGraph:
    def __init__(self):
        self.vertList = {}  # 这个虽然叫list但是实质上是字典
        self.numVertices = 0

    def addVertex(self, key):   # 增加节点
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

    def getVertex(self, key):   # 通过key获取节点信息
        if key in self.vertList:
            return self.vertList[key]
        else:
            return None

    def __contains__(self, n):  # 判断节点在不在图中
        return n in self.vertList

    def addEdge(self, from_key, to_key, cost=1):    # 新增边
        if from_key not in self.vertList:      # 不再图中的顶点先添加
            self.addVertex(from_key)
        if to_key not in self.vertList:
            self.addVertex(to_key)
        # 调用起始顶点的方法添加邻边
        self.vertList[from_key].addNeighbor(self.vertList[to_key], cost)

    def getVertices(self):   # 获取所有顶点的名称
        return self.vertList.keys()

    def __iter__(self):  # 迭代取出
        return iter(self.vertList.values())

    def Dijkstra(self, startVertex):   # 输入的stratVertex是节点的key
        startVertex = self.vertList[startVertex]
        startVertex.setDistance(0)
        startVertex.setPred(None)   # 将起始节点的前驱节点设置为None
        pq = Binheap()
        pq.buildHeap([(v, v.getDistance()) for v in self])
        while not pq.isEmpty():
            current_tuple = pq.delMin()
            for nextVertex in current_tuple[0].getConnections():
                newDistance = current_tuple[0].getDistance() +\
                                current_tuple[0].getWeight(nextVertex)
                # 如果当下一节点的dist属性大于当前节点加上边权值,就更新权值
                if newDistance < nextVertex.getDistance():
                    nextVertex.setDistance(newDistance)
            # 把更新好的值重新建队
            pq.buildHeap([(v[0], v[0].getDistance()) for v in pq])
            if not pq.isEmpty():
                # 把下一节点的前驱节点设置为当前节点
                nextVertex_set_pred = pq.findMin()[0]
                nextVertex_set_pred.setPred(current_tuple[0])

    def minDistance(self, from_key, to_key):
        self.Dijkstra(from_key)
        to_key = self.getVertex(to_key)
        min_distance = to_key.getDistance()
        while to_key.getPred():
            print(to_key.getId()+'<--', end='')
            to_key = to_key.getPred()
        print(from_key+' 最短距离为:', min_distance)

    def matrix(self, mat):    # 这里的mat用numpy传进来
        key = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
        for i in range(len(mat)):    # 邻接矩阵行表示from_key
            for j in range(len(mat)):  # 列表示to_key
                if i != j and mat[i, j] > 0:
                    self.addEdge(key[i], key[j], mat[i, j])

    def prim(self, startVertex):
        pq = Binheap()
        for v in self:
            v.setDistance(sys.maxsize)
            v.setPred(None)

        startVertex = self.vertList[startVertex]
        startVertex.setDistance(0)
        pq.buildHeap([(v, v.getDistance()) for v in self])
        while not pq.isEmpty():
            current_tuple = pq.delMin()
            for nextVertex in current_tuple[0].getConnections():
                # 注意这里是两顶点找最短边（因为是贪心算法）而不是找全局最短
                newWeight = current_tuple[0].getWeight(nextVertex)
                # 当这个节点在图中且新的权重比旧权重小，就更新权重，更新连接
                if nextVertex in pq and newWeight < nextVertex.getDistance():
                    nextVertex.setDistance(newWeight)
                    nextVertex.setPred(current_tuple[0])
                    # 对优先队列从新排列
                    pq.buildHeap([(v[0], v[0].getDistance()) for v in pq])
        for v in self:
            if v.getPred():
                print(f'节点{v.getId()}的前驱节点是{v.getPred().getId()}')


if __name__ == '__main__':
    DijGraph = DIJKSTRAGraph()
    inf = float('inf')
    a = np.array([[0, 1, 12, inf, inf, inf],
                  [inf, 0, 9, 3, inf, inf],
                  [inf, inf, 0, inf, 5, inf],
                  [inf, inf, 4, 0, 13, 15],
                  [inf, inf, inf, inf, 0, 4],
                  [inf, inf, inf, inf, inf, 0]])
    DijGraph.matrix(a)
    DijGraph.minDistance('A', 'F')
    DijGraph.prim('A')   # 输出最小生成树

写在最后

好啦，我这个阶段的图论笔记就到此为止啦，笔记里面当然有很多写的不好的地方，还有一些算法是没有实现的，比如那个欧拉道路的算法，感兴趣的同学写好了可以PULL到我的Github仓库， 也可以发邮件给我 我的个人邮箱是 395286447@qq.com

然后文章中出现的所有代码都在我的Github仓库里，潘登同学的Github仓库